 |
La
trajectoire
est l'ensemble des positions successives occupées par un point matériel
(ou un objet considéré comme un point) dans l'espace
au cours du temps. Elle est donc une courbe (dans
l'espace ou dans le plan) qui décrit comment un objet se déplace. Par
exemple, la trajectoire d'une balle lancée en l'air est une parabole
(dans le vide, sans résistance de l'air).
 Il
convient de distinguer le chemin, qui est la séquence géométrique
de positions (sans notion de temps), la trajectoire proprement dite
qui est le chemin paramétré dans le temps (inclut vitesse, accélération,
etc.), le déplacement qui est le vecteur allant de la position
initiale à la position finale (Δr = rf -
ri),
et la distance parcourue, qui est a longueur totale de la trajectoire
(scalaire, toujours positive). Par exemple, une personne qui fait un tour
complet autour d'un stade a une trajectoire circulaire, un déplacement
nul (retour au point de départ), mais une distance parcourue égale Ã
la circonférence. Il
convient de distinguer le chemin, qui est la séquence géométrique
de positions (sans notion de temps), la trajectoire proprement dite
qui est le chemin paramétré dans le temps (inclut vitesse, accélération,
etc.), le déplacement qui est le vecteur allant de la position
initiale à la position finale (Δr = rf -
ri),
et la distance parcourue, qui est a longueur totale de la trajectoire
(scalaire, toujours positive). Par exemple, une personne qui fait un tour
complet autour d'un stade a une trajectoire circulaire, un déplacement
nul (retour au point de départ), mais une distance parcourue égale Ã
la circonférence.
Représentation mathématique.
Termes
généraux.
Soit un espace euclidien 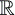 n.
On appelle trajectoire la courbe paramétrée décrite par une fonction
f : I n.
On appelle trajectoire la courbe paramétrée décrite par une fonction
f : I 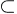 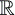 →
→ 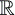 n,
t → f(t), où I est un intervalle réel et f est supposée au moins
continue, généralement dérivable. La variable t est interprétée comme
le paramètre d'évolution, typiquement le temps. Chaque point f(t) n,
t → f(t), où I est un intervalle réel et f est supposée au moins
continue, généralement dérivable. La variable t est interprétée comme
le paramètre d'évolution, typiquement le temps. Chaque point f(t) 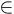 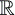 n
est
la position de l'objet ou du système à la date t. L'ensemble des points
atteints, appelé support de la trajectoire, est {f(t) | t n
est
la position de l'objet ou du système à la date t. L'ensemble des points
atteints, appelé support de la trajectoire, est {f(t) | t 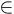 I}
I} 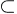 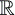 n.
Lorsque f est de classe C1 ( = fonction
numérique d'une variable réelle définie et dérivable sur un intervalle
donné, et dont la dérivée est continue sur ce même intervalle), la
vitesse
est définie comme la dérivée v(t) = f'(t) n.
Lorsque f est de classe C1 ( = fonction
numérique d'une variable réelle définie et dérivable sur un intervalle
donné, et dont la dérivée est continue sur ce même intervalle), la
vitesse
est définie comme la dérivée v(t) = f'(t) 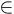 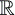 n,
qui indique la direction et la rapidité de déplacement. La norme ||v(t)||
donne la vitesse scalaire instantanée, et le vecteur accélération
est a(t) = f′′(t). Dans un cadre plus abstrait, si M est une variété
différentiable de dimension n, une trajectoire est une application différentiable
f : I → M, où chaque f(t) est un point de la variété. Cela permet
de décrire des mouvements dans des espaces non euclidiens, comme une sphère
ou un espace de configuration. n,
qui indique la direction et la rapidité de déplacement. La norme ||v(t)||
donne la vitesse scalaire instantanée, et le vecteur accélération
est a(t) = f′′(t). Dans un cadre plus abstrait, si M est une variété
différentiable de dimension n, une trajectoire est une application différentiable
f : I → M, où chaque f(t) est un point de la variété. Cela permet
de décrire des mouvements dans des espaces non euclidiens, comme une sphère
ou un espace de configuration.
Mécanique
classique.
En mécanique, la
trajectoire une courbe qui décrit la position de l'objet à chaque instant.
Pour formaliser cette notion, on utilise généralement des coordonnées
dans un repère, par exemple cartésien, polaire ou sphérique.
La position de l'objet
à un instant t est donnée par un vecteur r(t), où les composantes
dépendent des coordonnées choisies. Par exemple, dans l'espace euclidien
tridimensionnel muni d'un repère orthonormé (O, i, j, k),
on peut écrire : r(t) = x(t)i + y(t)j + z(t)k
,
où x(t), y(t), et z(t) sont les fonctions décrivant respectivement les
positions en abscisse, ordonnée et cote à l'instant t.
Le mouvement de l'objet
est gouverné par les lois de Newton, qui s'écrivent sous forme différentielle.
La deuxième loi de Newton stipule que la force F appliquée sur
l'objet est égale au produit de sa masse m par son accélération
a (F = ma), si m est constante.
L'accélération
étant la dérivée seconde de la position par rapport au temps, on obtient
l'équation : md²r/dt² = F(r, t). Cette équation
est une équation différentielle ordinaire (EDO) vectorielle, qu'il faut
résoudre pour déterminer la trajectoire exacte, ce qui nécessite des
conditions initiales : la position initiale r(0) et la vitesse initiale
v(0).
Une fois ces conditions fournies, on peut calculer les positions successives
r(t)
= (x(t), y(t), z(t)) pour tout t et tracer la trajectoire correspondante.
Dans certains cas,
on peut éliminer le temps pour obtenir une relation directe entre les
coordonnées spatiales : f(x, y, z) = 0. Dans le cas d'un mouvement sous
l'action d'une force centrale (comme pour un objet soumis à la gravitation),
la trajectoire peut être une conique (parabole, ellipse, hyperbole ou
droite). En particulier, pour un projectile sous l'effet de la pesanteur,
la trajectoire est une parabole si on néglige l'effet de la résistance
de l'air : y = xtan(θ) − gx²/ (2v0²​cos²(θ)​).
La trajectoire apparaît ainsi comme la solution géométrique de l'équation
du mouvement, qui dépend des forces agissant sur l'objet et des conditions
initiales. Elle peut être représentée graphiquement dans un espace Ã
trois dimensions ou projetée dans un plan selon les besoins.
Types de trajectoires.
Selon les forces
en jeu et les conditions initiales, on observe différents types de trajectoires
:
-
|
Type
de trajectoire
|
Contexte
typique
|
Forme
géométrique
|
| Rectiligne |
Mouvement
uniforme ou uniformément accéléré |
Droite |
| Parabolique |
Projectile
dans un champ gravitationnel uniforme |
Parabole |
| Circulaire |
Mouvement
uniforme autour d'un point |
Cercle |
| Elliptique |
Orbites
planétaires (selon Kepler) |
Ellipse |
| Hyperbolique
/ parabolique |
Trajectoires
non liées (ex. comètes) |
Hyperbole
ou parabole |
| Hélicoïdale |
Mouvement
combinant rotation et translation |
Hélice |
Relation de la
trajectoire avec les forces appliquées.
En mécanique
newtonienne, la trajectoire est déterminée par les conditions
initiales (position et vitesse initiales) et les forces appliquées (F
= dp/dt ou F= ma, si m est contante), où p
est la quantité de mouvement et m
la masse. La résolution de l'équation
différentielle du mouvement permet d'obtenir r(t) , donc la
trajectoire. Par exemple, dans un champ gravitationnel uniforme, l'accélération
g
est constante et la trajectoire parabolique.
Trajectoire dans
l'espace des phases.
Une trajectoire dans l'espace des phases
représente l'évolution d'un système
dynamique à travers une représentation qui combine les positions
et les vitesses (ou les impulsions) des objets ou des particules du système.
Chaque point dans cet espace correspond à un état particulier du système,
défini par les coordonnées et les vitesses associées aux différentes
composantes. Une trajectoire est donc la trace temporelle de cette évolution,
montrant comment l'état du système change avec le temps. Dans ce cadre,
les lois de mouvement du système se traduisent par des courbes ou des
surfaces dans cet espace multidimensionnel, permettant d'analyser les comportements
qualitatifs et quantitatifs du système, comme les points fixes, les cycles
limites ou les bifurcations.
Trajectoire des
ondes.
La trajectoire d'une
onde
est le chemin ou le parcours suivi par l'énergie
de cette onde à travers un milieu. Elle dépend des propriétés du milieu
dans lequel l'onde se propage, comme sa densité, sa composition ou encore
ses propriétés optiques. Dans le cas des ondes
lumineuses, par exemple, la trajectoire peut être influencée par
la réfraction ou la réflexion
lorsque l'onde traverse une interface entre deux milieux différents. Pour
les ondes mécaniques, telles que les ondes sonores, la trajectoire dépend
de la structure du milieu et des obstacles éventuels. La trajectoire peut
également être modifiée par des phénomènes tels que la diffraction
ou la réfraction.
Trajectoire en
mécanique céleste.
En astronomie, les
trajectoires des corps célestes sont régies par la loi de l'attraction
universelle ou par les équations de la relativité
générale (pour des précisions extrêmes). Selon l'énergie mécanique
totale, la trajectoire peut être :
• Elliptique
(énergie < 0 → orbite fermée),
• Parabolique
(énergie = 0 → trajectoire limite),
• Hyperbolique
(énergie > 0 → trajectoire ouverte).
Ces formes sont des
coniques, solutions des équations de Kepler.
Trajectoire en
physique quantique.
En mécanique quantique,
le concept de trajectoire classique disparaît. Selon le principe
d'indétermination de Heisenberg, on ne
peut pas connaître simultanément position et vitesse avec précision.
Les particules sont décrites par des fonctions d'onde, et leur "chemin"
est remplacé par des probabilités de présence. Certaines interprétations
(comme celle de Bohm) réintroduisent des trajectoires cachées, mais ce
n'est pas le cadre standard.
Trajectoire en
robotique et contrôle.
Dans la robotique,
la planification de trajectoire consiste à générer un chemin lisse,
réalisable et sécurisé pour un robot ou un bras articulé entre une
position de départ et une position d'arrivée, en respectant des contraintes
(vitesse, accélération, obstacles). |
|