Expressions mathématiques.
Il convient de distinguer la vitesse moyenne et la vitesse instantanée. 

Vitesse moyenne.
La notion de vitesse moyenne (vmoy)répond à la question : "Si l'objet avait maintenu un mouvement uniforme, quelle distance aurait-il parcourue par unité de temps?". On aura alors :  vmoy = (rf−ri)/(tf−ti) = Δr/Δt, où Δr est le déplacement (vecteur) et Δt est la durée du mouvement. 

Par exemple, si un véhicule parcourt 150 km en 2 heures, le module de sa vitesse moyenne est vmoy = 150 km/2 h = 75 km/h. La vitesse moyenne ne donne aucune information sur les détails du mouvement. Ainsi, une vitesse moyenne de 75 km/h ne dit pas si le véhicule roulé à vitesse constante ou s'il s'est arrêté dans les embouteillages.

v = lim Δr/Δt = dx /dt
   Δt→0

Sur un graphique de la position en fonction du temps (r(t)), la vitesse instantanée à un point est la pente de la tangente à la courbe en ce point.

Lle compteur de vitesse d'une voiture, par exemple, indique la vitesse instantanée, la vitesse à l'instant t.

Pour un mouvement en 3D (espace euclidien 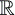³), le vecteur position s'écrit, dans un repère orthonormé (O, i, j, k) : r(t) = x(t)i + y(t)j +z(t)k. Le vecteur vitesse est alors :  v(t) = dr/dt = (dx/dt)i + (dy/dt)j + (dz/dt)k = vxi +vyj + vzk. Sa norme (vitesse scalaire) est : v =IIvII = √ (vx² + vy²+vz²).

La vitesse angulaire (pour les mouvements circulaires).
Pour un objet en rotation ou en mouvement circulaire, on dénit la vitesse angulaire, qui est l'angle θ balayé par unité de temps et se mesure dans le système international en radians par seconde (rad/s). La vitesse angulaire moyenne est  ωmoy =Δθ/Δt;  la vitesse angulaire instantanée est  ω = dθ/dt. Pour un mouvement circulaire de rayon R, la relation avec la vitesse est  v = Rω.

Importance du concept en mécanique.
En cinématique, la vitesse est la grandeur de base pour décrire tout mouvement. En dynamique, le taux de variation de la vitesse par rapport au temps (l'accélération) est liée aux forces par la deuxième loi de Newton (F = ma). par ailleurs, on peut définir l'énergie cinétique (l'énergie due au mouvement) d'un corps directement en fonction de la vitesse et de sa masse : Ec = 1/2mv².

La vitesse des ondes.
Différentes notions de vitesse sont associées aux ondes. Elles dépendent du type d'onde, du milieu traversé, et des conditions physiques spécifiques. 

• La vitesse de phase est la vitesse à laquelle une crête ou un point particulier d'une onde se déplace dans le temps. Elle est indépendante de l'amplitude de l'onde et ne dépend que de la fréquence de l'onde et des propriétés du milieu.

• La vitesse de propagation est ordinairement utilisée comme synonyme de vitesse de phase dans le cas des ondes simples. Cependant, elle peut également désigner la vitesse à laquelle l'onde se propage dans un milieu, qui dépend de la densité et de la rigidité élastique du milieu.

• La vitesse de groupe est la vitesse à laquelle l'énergie ou l'information se propage dans une onde. Elle est différente de la vitesse de phase, surtout pour les ondes composées de plusieurs fréquences, comme dans le cas des ondes cohérentes.

• Pour les ondes électromagnétiques, la vitesse de propagation dans le vide est constante et égale à la vitesse de la lumière (c = 299 792 458 m/s). Dans un milieu matériel, cette vitesse est réduite en raison de l'interaction des photons avec les particules du milieu.

La vitesse de la lumière dans le vide, généralement notée c, est une constante universelle fondamentale en physique. Cette vitesse joue un rôle central dans la théorie de la relativité restreinte d'Einstein et constitue une limite supérieure pour la propagation d'informations et d'énergie dans l'univers.

+ La découverte de la vitesse de la lumière a été progressive. Initialement, Galilée tenta de mesurer la vitesse de la lumière, mais sans succès, car elle est si élevée qu'il n'était pas possible de détecter un retard dans sa propagation. C'est Christiaan Huygens qui, au XVII^e siècle, proposa que la lumière se propageait sous forme d'ondes, une idée qui fut confirmée par des expériences ultérieures. En 1676, Ole Rømer mesura pour la première fois la vitesse de la lumière indirectement en observant les éclipses de Jupiter. Il remarqua que le retard dans ces éclipses variait selon la position de la Terre par rapport à Jupiter, ce qui permit de conclure que la lumière avait besoin de temps pour parcourir les distances interplanétaires. À la fin du XIX^e siècle, Albert Michelson et Edward Morley mirent en évidence que la lumière se propageait à la même vitesse, indépendamment du mouvement de la source ou du récepteur, ce qui mit en crise la notion de milieu éthéré, supposé être la substance invisible remplissant l'espace. Dans la théorie de la relativité restreinte d'Einstein, publiée en 1905, la vitesse de la lumière est considérée comme une constante absolue, indépendante du référentiel. Cette théorie introduit des concepts tels que la dilatation du temps et la contraction des longueurs, qui modifient notre perception de l'espace et du temps en fonction de la vitesse relative des objets. 

Dans un milieu matériel, la vitesse de la lumière diminue en raison de l'interaction des photons avec les particules du milieu. La vitesse effective de la lumière dans un matériau est donnée par v=c/n​, où n est l'indice de réfraction du matériau. La vitesse de la lumière influence également de nombreux phénomènes optiques, tels que la réflexion, la réfraction, la diffraction et la dispersion. La vitesse de la lumière intervient dans la comréhension des interactions entre la lumière et la matière. Elle est, de plus, intimement liée à la structure de l'univers, impliquée dans la formation des structures cosmologiques, et la propagation de l'influence des étoiles et galaxies lointaines.

Astronomie et cosmologie.
Le concept de vitesse en astronomie et en cosmologie revêt des significations et des interprétations différentes selon le contexte :

Vitesse en astronomie classique.
En astronomie locale (Système solaire, étoiles proches), la vitesse est définie comme en mécanique newtonienne : v = dr/dt, où r est la position d'un objet dans un repère inertiel (couramment centré sur la centre de la Terre, sur le Soleil, sur le barycentre du Système solaire, sur le centre de la Galaxie, etc.). On décompose alors la vitesse en deux composantes : vr, la vitesse radiale, qui est la composante de la vitesse le long de la ligne de visée (mesurée via l'effet Doppler), et vt, la vitesse tangentielle, qui est la composante perpendiculaire à la ligne de visée (mesurée via le mouvement propre et la distance). La vitesse spatiale v est la somme vectorielle deux : v = vr + vt.

Exemples : la Terre orbite autour du Soleil à ~30 km/s; le Soleil se déplace dans la Voie lactée à ~230 km/s par rapport au centre galactique. Les étoiles ont des vitesses relatives typiques de quelques dizaines à centaines de km/s par rapport au Soleil. 

La vitesse radiale est déduite de décalages spectraux en tenant compte des effets relativistes : ​λobs / λémis​ ​= √((1 + v/c) / (1 - v/c​)), pour mouvement radial).

Cas particuliers et paradoxes apparents.
Dans les quasars ou microquasars, des jets de plasma sont éjectés à des vitesses proches de c . On observe parfois une vitesse superluminique apparente due à un effet de projection (l'objet se déplace presque vers nous à v ≈ c). 

Vitesse en relativité générale et cosmologie.
Ici, le concept de vitesse devient subtil, car l'espace-temps lui-même est dynamique. On définit :

• La vitesse propre qui est la vitesse d'un objet par rapport au fluide cosmologique local (c'est-à-dire par rapport à l'expansion de l'Univers). Elle est due au champ de gravitation local (amas, galaxies, etc.) et est typiquement < 1000 km/s. 

• La vitesse de récession due à l'expansion cosmique. Dans l'univers en expansion (métrique de Friedmann-Lemaître-Robertson-Walker), la distance entre deux objets non liés gravitationnellement augmente avec le temps : D(t) = a(t).χ, où a(t)  est le facteur d'échelle et  χ  est la distance comobile (fixe). La vitesse de récession est alors : vrec​ = dD/dt = (t).χ= H(t).D(t), avec H(t) = Ã¥/a  le paramètre de Hubble. 

Loi de Hubble : vrec​ ≈ H0​⋅D  (pour distances modérées). 

Pendant l'inflation (très tôt dans l'Univers), l'espace s'est étendu exponentiellement en un temps très court. Les vitesses de récession associées étaient énormes, bien au-delà de c, mais encore une fois, sans violation de la relativité. 

Notons par ailleurs que le décalage vers le rouge (redshift z ) des objets lointains n'est pas dû à un mouvement Doppler classique, mais à l'expansion de l'espace pendant que la lumière voyage : 1+z = a(tobs​)/a(témis​)​. On peut interpréter ce redshift comme une vitesse de récession, mais ce n'est qu'une analogie utile à faible z.