Lorsqu'il s'agit de la distance d'un astre à la Terre, c'est une ligne droite tirée du centre de l'astre au centre de la Terre. Il en est souvent de même de la distance d'un astre au Soleil. S'il s'agit de la distance mutuelle de deux astres, ou d'un astre à un point quelconque du ciel  elle est mesurée par l'angle que forment entre elles deux lignes droites, tirées du centre de chacun de ces astres, à la Terre, ou par l'arc de cercle compris entre ces deux lignes. La mesure de cette distance est aussi quelquefois un arc de cercle compris entre les deux cercles de déclinaison ou de latitude, qui passent par les centres des deux astres. Par exemple, la distance mutuelle de deux astres en ascension droite, est l'arc de l'équateur compris entre les deux méridiens ou cercles de déclinaison, dont chacun passe par le centre de l'un des deux astres. De même la distance mutuelle de deux astres en longitude est l'arc, de l'écliptique, compris entre les deux cercles de latitude, dont chacun passe par le centre de l'un des deux astres (Coordonnées célestes). Deux sortes de distances angulaires peuvent également servir de coordonnées dans des systèmes de repérages des astres, la distance zénithale et la distance polaire : 

Distance zénithale. - La distance zénithale d'un astre est le complément de sa hauteur; c'est l'arc du cercle vertical de l'astre, compris entre l'astre et le zénith. Si l'on suppose que la distance polaire d' un astre reste constante, sa distance zénithale ne cesse de varier; elle diminue depuis le lever de l'astre jusqu'à son passage au méridien : elle augmente au contraire depuis le passage au méridien jusqu'au coucher de l'astre. La hauteur du même astre, quantité que l'on observe directement à l'aide du sextant, suit l'ordre inverse. Le même terme s'emploie en topographie; la distance zénithale d'un point du terrain, visé d'une station topographique, est l'angle vertical compris entre cette visée et le zénith.

Distance polaire. - La distance polaire est la distance de l'astre au pôle élevé, comptée sur le cercle de déclinaison. Elle varie entre 0° et 180°. Cette quantité était utilisée couramment  dans les calculs nautiques.

Diamètre apparent d'un astre. - Angle sous lequel, de la Terre, on voit cet astre. Cet angle varie avec la distance réelle de l'astre. Ainsi, le diamètre apparent du Soleil à la fin de décembre, au moment du périhélie, est de 32' 36"; au commencement de juillet, époque de l'aphélie, il est de 31' 31".

La parallaxe diurne et parallaxe annuelle sont des notions qui relèvent de la méthode de détermination des distances dite méthode des parallaxes trigonométriques. Elle vaut pour connaître la distance des objets du Système solaire, et surtout celle des étoiles les plus proches situées dans notre Galaxie. Sachant, grâce à cela calculer l'éclat réel d'une étoile de type donné à partir de son éclat apparent, on va pouvoir évaluer des distances au-delà du domaine où la méthode des parallaxes est utilisable. De nouvelles méthodes, avec des domaines d'applications définis pourront encore être utilisées. Et d'autres encore, qui reposeront sur celles-ci, etc. Beaucoup de possibilités sont ainsi offertes en pratique. Parfois, elles s'utilisent pour se corroborer mutuellement, mais toutes pâtissent du même vice : reposant sur les données obtenues à partir des méthodes sur lesquelles elles reposent, elles héritent des inévitables incertitudes que contiennent leurs assises. Il s'ensuit que plus les objets étudiés sont distants, et plus la connaissance de leur distance devient incertaine. 

La parallaxe est un angle qui dénote un effet de perspective. Celui-ci peut provenir de ce que l'on observe un astre de deux positions différentes à la surface de la Terre, ou de deux positions différentes le long de l'orbite terrestre autour du Soleil. On peut ainsi entendre en particulier la parallaxe dans deux acceptions différentes, selon que l'on considère la rotation de la Terre, qui amène un observateur, à 12 heures d'intervalle, à deux positions séparées d'un diamètre terrestre, ou que l'on considère le mouvement de révolution annuelle autour du Soleil, qui, à six mois d'intervalle, amènera un observateur placé à la surface de la Terre aux deux points extrêmes de son orbite.  Cela servira à définir respectivement la parallaxe diurne et la parallaxe annuelle, qui est le support de la détermination des parallaxes stellaires.

La parallaxe diurne.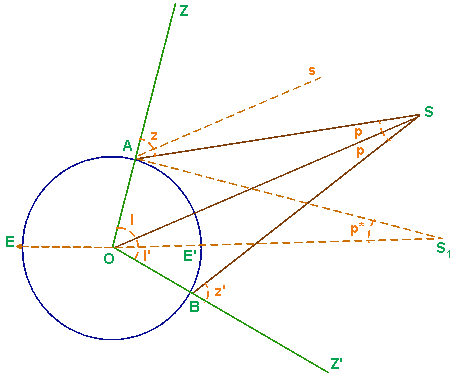
La parallaxe diurne d'un astre, relativement à un lieu de la Terre, est l'angle sous lequel serait vu, du centre même de l'astre, le rayon de la Terre. Cette parallaxe est dite horizontale quand cet astre se trouve dans le plan tangent au globe mené par l'extrémité du rayon que l'on considère, et, parallaxe de hauteur, quand le même point est au-dessus de ce plan. Voici comment cela se présente dans le détail :
-

Lorsque l'astre est au zénith, la parallaxe est évidemment nulle, les deux rayons visuels se confondant suivant OZ. Au fur et à mesure qu'il se rapproche de l'horizon, elle grandit, et elle atteint son maximum au moment de son lever ou de son coucher, lorsqu'il est exactement à l'horizon, en S' par exemple. On lui donne, dans ce dernier cas, le nom de parallaxe horizontale. Elle est dite, au contraire, parallaxe de hauteur pour toutes les autres positions de l'astre. La parallaxe de hauteur et la parallaxe horizontale d'un même astre sont liées entre elles par une relation très simple, qui permet de passer aisément de l'une à l'autre. Appelons p la parallaxe de hauteur ASO, p' la parallaxe horizontale AS'O, r le rayon terrestre OA, d la distance OS du centre de la Terre à l'astre, z la distance zénithale SAZ, supposée corrigée de la réfraction astronomique. Dans le triangle AOS, on a  :

Dans le triangle rectangle AS'O, on a :

En rapprochant [1] et [2],  il vient  : 

ou encore, p et p' étant toujours assez petits pour être pris pour leurs sinus :

La parallaxe de hauteur est donc égale à la parallaxe horizontale multipliée par le sinus de la distance zénithale. D'autre, part, d'après la formule [1] :

ou, p étant, nous venons de le dire, toujours très petit, :

Supposons maintenant que deux observateurs se portent en deux stations éloignées choisies sur un même méridien, A et B, de latitudes l et l', par rapport à l'équateur EE'. A l'instant du passage de l'astre au méridien, en S, ils prendront les distances zénithales z et z', supposées corrigées de la réfraction astronomique. Soient p et p* les parallaxes de hauteur ASO et BSO. On aura, d'après la formule [4],

Additionnons les quatre angles du quadrilatère ASBO. Leur somme est égale à quatre droits ou à 360°.0n peut donc écrire, en remarquant que SAO est le supplément de z et SBO le supplément de z' :

d'où 

Or r/d n'est autre chose, d'après la formule [2], que sin p' et, p' étant toujours très petit, que p' lui-même, c'est-à-dire que la parallaxe horizontale. De celle-ci on déduit, suivant la formule [3], la parallaxe de hauteur, sans avoir en besoin de connaître, à aucun moment, la distance d de la terre à l'astre, et, suivant la formule [2], cette distance elle-même. C'est même là le principal intérêt pratique du calcul des parallaxes. Elles servent aussi à ramener au centre de la Terre les observations faites en un point de sa surface.

La Caille et Lalande ont déterminé, par la méthode qui précède, en se plaçant respectivement au cap de Bonne-Espérance et à Berlin, la parallaxe de la Lune, celle de Vénus et celle de Mars. La même méthode a été appliquée, par la suite, aux autres planètes, quoiqu'il est paru préférable de déduire leurs parallaxes de celle du Soleil. Du moins jusqu'en 1898-99, quand la découverte du premier circastéroïde, Éros, a permis d'espérer une précision accrue des mesures, lors des ses passages au plus près de la Terre. En 1931, en particulier, celui-ci s'est approché à 22 millions de kilomètres de notre planète, ce qui lui donnait une parallaxe de 60" et conduisait à attribuer au Soleil une parallaxe horizontale de p° = 8,790", à un centième de seconde près.

D'autres méthodes ont encore été employées pour la détermination de la parallaxe de la Lune : celle des plus grandes latitudes, dont Ptolémée, Tycho Brahé et Halley ont fait usage; celle des parallaxes d'ascension droite, qu'on trouve exposée dans l'ouvrage de Regiomontanussur les planètes et qui a successivement servi à Thomas Digges (1573), à Kepler (1649), à Flamsteed (1672), à Cassini (1684): enfin celle des éclipses.

Pour le Soleil, l'observation directe ne donnerait, en égard à son éloignement, qu'une approximation insuffisante. On doit on a donc eu historiquement recours à d'autres méthodes, soit à celle des quadratures de la Lune, soit à celle des passages de Vénus ou de Mercure. Les passages de Mercure ne donnent pas, d'ailleurs, des résultats suffisamment concluants et la préférence a été donnée à la méthode des passages de Vénus (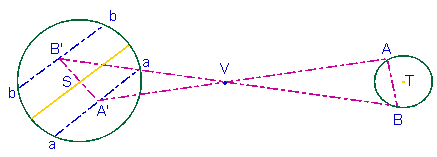Les passages de Vénus devant le Soleil). 

Mais le rapport AV / A'V se déduit facilement du rapport des distances de la Terre et de Vénus au Soleil, lequel est donné par la troisième loi de Kepler. On connaîtra donc le rapport AB/A'B' et, en évaluant l'angle sous lequel la corde A'B' est vue de la Terre, l'angle sous lequel la corde AB serait vue elle-même du Soleil. Il ne restera plus qu'à calculer cette corde AB au moyen des coordonnées géographiques de A et de B et à en déduire, à l'aide d'une simple proportion, l'angle sous lequel le rayon terrestre serait vu de la même distance, c.-à-d. la parallaxe horizontale du Soleil. Pour d'aussi longues distances, en effet, les angles sous lesquels sont vues deux longueurs, relativement très petites, sont sensiblement proportionnels à ces longueurs. Quant à la parallaxe de hauteur, elle sera fournie ensuite par la formule [3]. Il n'est, du reste, pas indispensable que les deux stations soient, comme nous l'avons supposé, aux extrémités d'une même corde perpendiculaire à l'écliptique. On peut les prendre quelconques, en faisant, s'il y a lieu, les corrections nécessaires. Il faut seulement éviter que les deux traces de la planète sur le disque soient trop petites ou trop rapprochées.

Cette méthode a été imaginée en 1691 par Halley, qui l'a publiée en 1694. Elle a été appliquée, pour la première fois, aux passages de 1764 et 1769, et la parallaxe moyenne horizontale du Soleil avait d'abord été fixée, d'après ses résultats, à 8",57. Mais Le Verrier, après de nouveaux calculs, l'avait portée à 8",86. Par la suite, de nouvelles observations ont été faites durant les passages de 1874 et de 1882, et leur discussion a indiqué, en tenant compte de la valeur de l'aberration, 8",798 d'après Cornu, 8',794, d'après Newcomb. Un simple écart de 0,01", en plus ou en moins, dans cette évaluation, produit, d'ailleurs, une diminution ou une augmentation de 170 000 kilomètres dans la distance du Soleil à la Terre. Aussi les idées des anciens étaient-elles, à cet égard, très grossières. Aristarque de Samos, qui, vers 264 av. avait voulu calculer la parallaxe 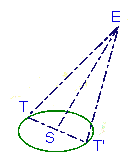du Soleil, avait trouvé 3' et il en avait conclu une distance de 1146 rayons terrestres seulement. On en devait rester là pendant plus de dix-huit siècles.

On opère de la façon suivante. Soit E l'étoile considérée, S le soleil, T et T' les positions occupées par la Terre sur son orbite, aux deux époques de l'année où sa longitude diffère de 90° de celle de l'étoile, c.-à-d. ou TSE et T'SE sont des angles droits. On détermine les angles STE et ST'E formés par les rayons visuels menés de la Terre au Soleil et à l'étoile; on en déduit, dans les triangles rectangles TES et T'ES, les angles TES et T'ES,  égaux l'un et l'autre à la parallaxe annuelle de l'étoile. La distance de la Terre à l'étoile est donnée ensuite par les hypoténuses TE et T'E des mêmes triangles. (L. Barré).

Les étoiles les plus proches du Système solaire - celles dont la parallaxe est la plus grande - ont des parallaxes qui ne dépassent pas les 0,8" d'arc. C'est dire que la détermination des parallaxes stellaires est particulièrement difficile, et pendant très longtemps, les incertitudes on dépassé un ou même parfois plusieurs dixièmes de seconde. La situation s'est améliorée au fil du temps, et est devenue bien meilleure depuis l'achèvement, à la fin des années 1990, du programme du satellite astrométrique Hipparcos. 

L'idée de se servir du mouvement annuel de la Terre pour déterminer les distances qui la séparent des étoiles remonte à Copernic, qui y cherchait en outre une démonstration directe de la vérité de son système. Mais les observations faites par Tycho Brahé dans ce but ne lui ont montré aucune variation de ce genre, malgré tout le soin qu'il y avait apporté. Il en fut ainsi pendant très longtemps pour toutes les tentatives successives de Hooke, Picard, J.-D. Cassini, Flamsteed, J. Cassini, Roemer et Manfredi, jusqu'à ce que Bradley ait démontré que l'effet du déplacement annuel de la Terre sur les lieux apparents des étoiles est complexe et que sa partie importante ne tient pas au changement de position de notre globe, mais est un effet du déplacement à une vitesse finie de la lumière, nommé aberration.

Malgré les efforts de plusieurs générations d'astronomes - parmi lesquels on citera les noms de Brinkley, Lalande,  Lindenau, W. Struve, Arago et Mathieu, Piazzi, etc., il faudra attendre les premières années du XIXe siècle pour que l'on dispose de la première mesure admissible et reconnue exacte, celle d'une étoile de de magnitude 6, à peine visible à l'oeil nu, 61 Cygni (Cygne), qui avait attiré l'attention par son mouvement propre important. C'est Bessel qui fit cette mesure en 1838. Il trouva 0"374 pour la parallaxe de l'étoile, ce qui lui fournit pour la distance au Soleil 551 000 fois le rayon de l'orbite terrestre, on environ 81 000 milliards de kilomètres. La troisième parallaxe stellaire fut déterminée par W. Struve en 1840; c'était celle de Véga (Lyre). Mais auparavant, Thomas Henderson, en 1839 avait mesuré la distance de Toliman (Alpha du Centaure). Cette parallaxe, la seconde donc à avoir été mesurée, atteint 0"9 environ. Elle correspondra à la plus grande valeur obtenue, désignant ainsi l'étoile la plus proche du Soleil, jusqu'à la découverte, dans la même région du ciel par R. T. Innes, en 1915, de Proxima Centauri. Cette naine rouge (Les Mini-étoiles), 13 000 fois moins lumineuse que le Soleil, restera certainement très longtemps l'étoile ordinaire la plus proche du Système solaire. Il n'est cependant pas exclu que des objets plus exotiques, et moins lumineux (naines brunes, et pourquoi pas trous noirs...), puissent être découverts encore plus près de nous.
-
Vue d'artiste du satellite Hipparcos.
(Source  : Esa, Science & Technology).

Les mesures de parallaxes stellaires ont été péniblement continuées tout au long du XXe siècle. Les astronomes disposaient de moins de dix mille parallaxes stellaires plus ou moins précises  - moins de cinq mille connues avec une incertitude inférieure à 10%, moins de mille avec une incertitude inférieure à 5% -, quand à été lancé en 1989,  par l'Agence spatiale européenne, le satellite astrométrique Hipparcos. Ce satellite (dont le nom, qui fait bien sûr référence à ce grand ancêtre de l'astrométrie qu'a été Hipparque, est l'acronyme de High precision parallax collectingsatellite), a fonctionné entre novembre 1989 et mars 1993. Travailler depuis l'espace, c'est-à-dire en s'affranchissant des perturbations atmosphériques, a permis de recueillir des données d'une précision sans précédent. Un premier catalogue (Hipparcos fondamental) contient - accompagnées de mesures photométriques et de mesures de mouvements propres - les mesures de 118 000 parallaxes stellaires, données avec une précision de 25 millisecondes d'arc. Deux autres catalogues, publiés ensuite, (Tycho-1 et Tycho-2), fournissent les mêmes informations, avec une précision typiquement vingt fois inférieure, mais cette fois pour 1 million et 2,5 millions d'astres, respectivement. Du fait du caractère fondamental des parallaxes trigonométriques, l'impact sur toute l'astronomie de ces résultats récents est déjà considérable. 
 

Les parallaxes séculaires. La méthode des parallaxes séculaires (aussi appelées parallaxes statistiques ou hypothétiques)  est une méthode statistique seulement utilisable pour déterminer la distance de groupes d'étoiles. Son principe repose non plus sur le déplacement de la Terre autour du Soleil, mais sur celui du Système solaire tout entier dans la Galaxie, ce déplacement faisant apparaître un effet systématique sur le mouvement propre des autres étoiles.

Les parallaxes cinématiques. La méthode mise en oeuvre ici prend le nom de méthode du point de convergence. Comme dans le cas des parallaxes trigonométriques, c'est encore un effet de perspective que l'on mesure, et comme dans celui des parallaxes séculaires, c'est à un groupe d'étoiles qu'on l'applique (cela explique que l'on parle de parallaxes statistiques aussi dans ce cas). Mais cette fois, les étoiles concernées appartiennent à un même amas et ont supposées se déplacer toutes dans la même direction. L'effet de perspective en question correspond au fait qu'au lieu de paraître parallèles, les mouvements de ces étoiles paraissent converger ver un point unique (de la même façon que les rails parallèles d'un chemin de fer semblent se rencontrer à l'horizon). La distance est déduite de la mesure de cette convergence. La méthode a été utilisée pour évaluer la distance d'une poignée d'amas ouverts proches du Système solaire : l'amas de la Grande Ourse, des amas dans le Scorpion et le Centaure, et surtout l'amas des Hyades (Taureau), qui joue un rôle de marche-pied important pour l'établissement des indicateurs de distances secondaires. 

Les indicateur de distance secondaires sont fournis par des méthodes qui reposent sur la mesure de quantités dont le rapport à la distance est fourni de façon théorique, sur la base de quantités établies à partir des indicateurs primaires (parallaxes géométriques). La plupart du temps, elles reposent sur la mesure de la luminosité apparente de l'astre, que l'on rapporte à la luminosité intrinsèque que la théorie utilisée lui attribue. Sachant que la luminosité apparente d'un astre variant comme l'inverse du carré de sa distance, on en déduira immédiatement cette dernière. Lorsqu'on adopte une telle approche, on constate que tous les astres ne conviennent pas - leur luminosité intrinsèque ne se lit pas sur leur figure... - Ceux qui conviennent sont appelés des chandelles standard. Ce sont des objets dont on peut déduire la luminosité réelle de leur spectre dans le cas d'un certain nombre d'étoiles, de leur période de pulsations, pour quelques types de variables, de diverses caractéristiques photométriques dans le cas de galaxies, etc. 

Une fois que l'on sait que tous les astres d'une certaine catégorie (définie par les critères précédents) ont  une luminosité intrinsèque calculable - ce qui en fait donc des chandelles standard - on doit se préoccuper d'étalonner le nouvel instrument de mesure qu'ils procurent. Et c'est ici, que les parallaxes géométriques, indicateurs primaires de distance interviennent, ou, à défaut, d'autres indicateurs secondaires dont l'étalonnage a déjà été effectué.

Les méthodes spectroscopiques.
Ces méthodes permettent de déduire la valeur de la magnitude absolue de l'astre ou des astres dont on veut connaître la distance à partir de caractéristiques tirées de leur spectre : type spectral, échelle du diagramme HR, en particulier :

La parallaxe spectroscopique. - Malgré ce que suggère son nom, cette méthode n'a rien de géométrique. Elle consiste simplement à comparer la magnitude apparente de l'étoile considérée avec la valeur de sa magnitude absolue, que l'on déduit de son type spectral.  Cela conduit, au passage, à définir une pseudo-unité de distance, le module de distance µ, qui est la différence entre la magnitude apparente  m et la magnitude absolue M, soit µ= m-M. On relie le module de distance la distance p mesurée en parsecs (voir plus bas) par la formule :

Cette méthode, très simple, est peu précise, car le type spectral, qui requiert de grandes dispersions, et donc des étoiles relativement brillantes, n'est pas toujours connu avec la précision voulue. 

L'ajustement de la séquence principale. - Proche de la précédente, cette méthode utilisable pour mesurer la distance des amas stellaires est plus précise grâce à l'effet de nombre. Elle repose sur la comparaison du diagramme HR observé de l'amas, ou figurent les magnitudes apparentes des étoiles en fonction de leur couleur,  avec un diagramme HR théorique valable pour le groupe d'étoiles considérées, et ou figurent cette fois les magnitudes absolues. Il suffit de faire glisser les deux diagrammes l'un sur l'autre jusqu'à ce que les points points représentatifs des étoiles de la séquence principale se superposent. La mesure du décalage entre magnitudes observées et magnitudes absolues donne directement la distance cherchée. 

Les méthodes photométriques.
Il s'agit dans ces méthodes, dont la validité est d'ordre statistique, de se baser sur la façon dont se distribuent les luminosités des astres qui constituent une galaxies lointaine. On utilisera comme pour indicateur de distance, par exemple l'objet le plus brillant d'un type particulier, ou  même la répartitions de la luminosité de la totalité des étoiles de la galaxie concernée : 

L'objet le plus brillant.- L'idée de cette méthode, utilisée pour évaluer la distance des autres galaxies, repose sur l'hypothèse qu'il existe une luminosité maximale pour les astres d'une catégorie particulière (la luminosité d'une géante rouge, d'une région II, (dont on pourra aussi tirer une indication de son diamètre) d'un amas globulaire, etc., ne peut pas être indéfiniment grande...). On essaie donc de repérer dans la galaxie considérée LE  "monstre" de sa catégorie, auquel on attribuera une magnitude absolue probable, et l'on procédera ensuite comme avec la méthode des parallaxes spectroscopiques.

La fonction de luminosité. -  De la même façon que la méthode de l'ajustement de la séquence principale améliore par l'effet de nombre la méthode des parallaxes spectroscopique, la méthode basée sur la fonction de luminosité procure une sûreté meilleure que la méthode de l'objet le plus brillant. Dans le cas présent, on considère que, statistiquement, tous les astres d'une même catégorie ont des luminosités qui se distribuent de la même façon. la fonction de luminosité exprime que pour un échantillon donné, il y a tel pourcentage d'objets dans une fourchette de luminosité, et tel autre pourcentage pour telle autre fourchette. En comparant une fois de plus la distribution des magnitudes apparentes à une distribution attendue, on pourra donc calculer ici encore la distance de l'échantillon. La méthode peut être utilisé avec les galaxies spirales dans un même amas, avec les nébuleuses planétaires d'une même galaxie, ainsi d'ailleurs qu'avec toutes les étoiles d'une même galaxie (méthode dite des fluctuations de brillance de surface). 

Les méthodes applicables aux étoiles variables. 
Les variations d'éclat de certaines étoiles variables sont directement liées à leur magnitude intrinsèque. Les variables dont l'enveloppe connaît des pulsations obéissent par exemple à des relations entre leur période et leur luminosité; et pour leur part, les explosions des novae et les supernovae peuvent révéler une relation entre leur luminosité au moment où elles sont le plus brillantes et la manière dont leur lumière décline ensuite :

La relation période-luminosité. - L'existence de cette relation est particulièrement utile dans le cas des variables pulsantes, que ce soit les céphéides ou les RR Lyrae. Celles des céphéides a été découverte en 1912 par Henrietta Leavitt alors qu'elle les variables du Petit Nuage de Magellan (Toucan), et a été utilisée dans les décennies suivantes pour mettre sur pied une échelle des distances extragalactiques. Il suffit dans ce cas de mesurer le temps que dure la pulsation d'une céphéide repérée dans la galaxie étudiée pour calculer sa magnitude absolue, et, par comparaison avec sa magnitude apparente, pour obtenir son module de distance. 

La méthode de Baade-Wesselink, également applicable aux étoiles pulsantes repose sur la relation entre leur magnitude absolue et l'évolution de leur couleur.

Le déclin lumineux. - Certaines variables cataclysmiques, telles les novae et certaines supernovae, sont susceptibles d'être abordées la même façon. Leur variation d'éclat n'est évidemment pas périodique, mais la courbe de décroissance de leur lumière, rapportée à leur maximum de luminosité, peut informer sur leur magnitude absolue. Une telle relation mise en évidence par Phillips pour les supernovae de type Ia est utilisée pour évaluer les distances des supernovae les plus lointaines jamais observées. Sa validité est actuellement au centre de nombreuses préoccupations, car c'est par elle qu'a été mise en évidence depuis 1998 la possible accélération de l'expansion cosmique.

Les méthodes dynamiques.
Dans ces méthodes, de nature statistique, l'indicateur de distance est la distribution des  vitesses des objets que contient un galaxie ou un amas globulaire : 

La relation de Tully-Fisher. - Déjà soupçonnée par Opik, en 1922, puis établie par Tully et Fisher en 1977, cette relation repose sur le fait que la vitesse de rotation d'une galaxie spirale est proportionnelle à la masse de la galaxie. La vitesse est directement mesurée par effet Doppler, et de la masse on déduit la magnitude intrinsèque de la galaxie. 

La relation de Faber-Jackson (1976). Elle est analogue à la relation de Tully-Fisher, mais concerne les galaxies elliptiques. 

La dispersion des vitesses dans les amas globulaires. En 1992, Paturel et Garnier ont montré que la dispersion de la vitesse radiale des étoiles d'un amas globulaires pouvait être reliée à sa magnitude absolue.

Les distances cosmologiques

Dès que l'on dépasse les limites de la Voie lactée, on pourrait déjà parler de distances cosmologiques, et nombres des indicateurs précédemment mentionnés jouent un rôle important dans la mesure des distances extragalactiques. Mais il existe encore d'autres des approches de l'univers à grande échelle, qui ont la particularité de ne nécessiter aucune calibration. Elles donnent directement des mesures de distances, un peu comme les méthodes parallactiques, et toujours à partir de bases géométriques, mais cette fois une perspective bien différente. On ne fera que mentionner la méthode qui utilise le décalage dans le temps entre les fluctuations de la luminosité d'un quasar lointain, lorsque sa lumière subit l'effet d'une lentille gravitationnelle, et la méthode qui utilise l'effet Sunyaev - Zeldovich (celui-ci correspond à l'interaction des photons du fond diffus cosmologique avec le gaz chaud dans lequel baignent les amas de galaxies). La méthode la plus connue et la plus simple reste cependant celle qui recours à la loi de Hubble, dont l'indicateur de distance est le décalage spectral* vers le rouge, ou redshift*, quantité directement mesurable sur un spectre. Ce phénomène, qui est une conséquence de l'expansion de l'univers, est d'autant plus marqué que les objets considérés sont distants. 

La Loi de Hubble. Proposée en 1929 par Edwin Hubble, la loi qui porte son nom rend compte de la manière dont toutes les galaxies lointaines semblent s'éloigner de nous, avec des vitesses proportionnelles à leurs distances. Ce que l'on exprime sous la forme : 

où v est la vitesse radiale, H un paramètre appelé la constante de Hubble, et d la distance. Si tout cela ne concernait pas un univers en expansion, le sens de chaque paramètre serait assez transparent. En réalité, tout dans cette formule est problématique : comment mesure-t-on v? Que vaut H?, et, d'abord, à quoi correspond véritablement d? de quelle distance parle-t-on : de celle de l'objet quand il a émis la lumière qui nous en parvient? de celle qui est la sienne aujourd'hui, étant entendu que l'expansion l'a considérablement éloigné depuis qu'il a émis sa lumière? ou bien de la distance parcourue effectivement par sa lumière? Admettons que ce soit cette dernière quantité que l'on considère, reste encore à connaître la valeur de H, qui dans un univers en expansion correspond à son taux d'expansion, et qui varie en fait dans le temps (voire éventuellement dans la direction où on la mesure), selon une loi également fonction de la géométrie globale de l'univers (dont la connaissance est l'objectif premier de la cosmologie!).

La valeur de H_°. - Non seulement H varie avec le temps, mais sa valeur actuelle, notée  H_°, n'est pas simple à déterminée. Hubble s'était trompé d'un facteur dix dans son évaluation, après lui, et jusqu'à récemment sa valeur était comprise dans une fourchette qui allait du simple au double. Dans le système d'unités habituellement utilisé (km/s/Mpc) elle allait de 50 à 100. En 2001, l'équipe des chercheurs qui travaillaient à la détermination de H_° à l'aide du télescope spatial Hubble on publié la valeur de 72 (à huit unités près, en plus ou en moins) et, en 2003, les indications fournies par le satellite MAP, conduisent à la valeur de 71 (à quatre unités près). 

Redshift. - Ce terme s'emploie spécialement pour désigner le décalage affecté par les longueurs d'onde d'un rayonnement soumis à un champ de gravitation. Lorsqu'il s'agit de l'effet du champ de gravitation global de l'univers, et le redshift traduit l'expansion cosmique (ce que l'on précise parfois en le désignant sous le nom de redshift cosmologique).

où c est la vitesse de la lumière dans le vide, z le redshift, H, le paramètre de Hubble, et d la distance (longueur du trajet du rayon lumineux). Le redshift z et la distance d peuvent toujours être rapportés à une distance définie plus classiquement, dès qu'un modèle particulier d'univers est adopté. Actuellement les galaxies les plus lointaines que l'on connaisse se situent un peu au-delà de  z = 6,5. Selon une annonce faite à la mi-février 2004, une galaxie, découverte grâce à l'amplification de sa lumière par effet de lentille gravitationnelle dans la direction de l'amas Abell 2218 (Dragon), semble même se situer à un redshift compris entre z = 6,6 et z = 7,1. Si l'on adopte les paramètres cosmologiques les plus plus courants, cela en ferait un objet situé à plus de 13 milliards d'années-lumière de nous, et formé seulement  quelque 750 à 800  millions d'années après le big bang.

Dans le cas des objets du Système solaire,  les distances ont d'abord été évaluées de façon géométrique, par la mesure des parallaxes, et en particulier par celle du Soleil, qui donnait la clé de toutes les autres dont la clé pouvait être donnée par la troisième loi de Kepler*. Celle-ci énonce en effet, que les carrés des temps de révolution des planètes sont proportionnels au cube des demi-grand axes des ellipses que tracent leurs orbites. Dès lors, si l'on connaît la mesure du rayon moyen d'une seule planète, les valeurs des autres rayons se déduira simplement de leur durée de révolution, facile à déterminer. La durée se mesurant le plus communément en années, c'est-à-dire en durées de la période de révolution de la Terre, il paraissait naturel de choisir pour unité de distance dans le système solaire, la distance moyenne de notre planète au Soleil. C'est ainsi que se définit l'unité astronomique*.

Unité astronomique. - L'unité astronomique (symbole : ua) est l'unité couramment utilisée pour définir les distances dans le Système solaire. Longtemps définie comme la distance moyenne de la Terre au Soleil, elle possède aujourd'hui une définition dynamique, plus proche de sa logique originelle, puisque fondée sur la troisième loi de Kepler :

a = (k² (1+m) /n²)^1/2

où a est le demi grand axe de l'orbite terrestre, n le moyen mouvement sidéral (en radians par jour), k, la constante de gravitation gaussienne, et m, la masse de la planète (exprimée en unités de masse solaire).  Depuis 1970, on adopte la valeur : 1 ua = 149,597870 millions de kilomètres. 

Ajoutons que le laser est également utilisé (toujours par la méthode de l'écho) pour mesurer la distance de la Lune, (384 403 km) depuis que des réflecteurs y ont été déposé à cet effet à l'occasion de la première expédition Apollo (L'exploration de la Lune). Ces mesures sont précises à quelques centimètres près, et l'on sait grâce à elles que notre satellite s'éloigne de la Terre de 3,74 cm par an.

Le tableau suivant donnent les distances au Soleil des principaux objets du Système solaire en unités astronomiques et en millions de kilomètres. Sont également données leurs périodes de révolution, exprimées en années :
-

Parsec. - Le parsec (symbole : pc) est la distance à laquelle un astre présente une parallaxe annuelle d'une seconde d'arc. Autrement dit, si l'on note que pour les petits angles, la valeur du sinus et la mesure de l'angle (en radians) se confondent, une  distance D, exprimée en parsecs, correspond simplement à l'inverse d'une parallaxe p, exprimée en secondes d'arc : D = 1/p. Il s'ensuit qu'un parsec est égal à 206, 265 unités astronomiques, soit 30,8568 millions de millions de kilomètres. Pour parler de distances de galaxies, on utilise le plus souvent pour unités le kiloparsec (kpc) et le mégaparsec (Mpc), qui vaut un million de parsecs.

Année-lumière (appelée aussi année de lumière par les puristes). - L'année-lumière (symbole : al) est la distance parcourue par la lumière dans le vide en une année - soit environ : 9 461 000 000 000 kilomètres. Pour les distances courtes, on peut utiliser des subdivisions de l'année, ainsi pourra-t-on lire que la Soleil se situe à seulement 8 mn 20 s de lumière de la Terre, ou que Saturne est à cinq heures de lumière. On ne parle pas, en revanche de décennies ou de siècles-lumière, mais les objets les plus lointains sont à des distances qui dépassent la dizaine de milliards d'années-lumière.

Le tableau suivant donne les distances, exprimées en années-lumière, des vingt étoiles les plus proches et des vingt les plus brillantes du ciel. Notez les disparités entre ces deux ensembles, dues à de très grands écarts dans la luminosité des étoiles. Les objets qui se trouvent à la fois parmi les plus proches et les plus brillants sont en gras : 
-

L'année-lumière est-elle plus intuitive que le parsec? Pas si sûr. C'est d'abord une affaire d'habitude. Une chose est sûre, les deux unités conservent la même connotation "géo-héliocentrique",  l'une faisant allusion très narcissiquement à la taille apparente de son orbite terrestre autour du Soleil, l'autre à la période de révolution de notre planète. D'une manière ou d'une autre, le cosmos doit rester à la mesure de l'humain! Pour le non-spécialiste l'année-lumière a cependant cet avantage qu'elle donne directement accès à ce que les cosmologistes appellent le temps de regard en arrière, qui renvoie au fait que plus on regarde loin, et plus on voit des objets tels qu'ils étaient dans un passé reculé. Une galaxie située, par exemple, à cinq milliards d'années-lumière nous apparaît comme elle était il y a cinq milliards d'années. Et l'on peut comprendre que, puisque l'univers est vieux tout au plus d'une quinzaine de milliards d'années, on ne ne peut pas observer d'astre situé à une distance supérieure à quinze milliards d'années-lumière (ce qui ne signifie nullement que l'univers ne puisse être beaucoup plus grand).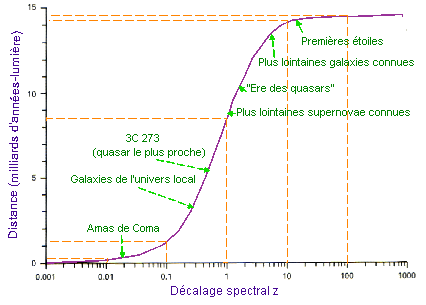 

Équivalence approximative des distances et des décalages spectraux,
dans un univers supposé vieux de 15 milliards d'années.