-

La pensée et ses outils > Philosophie > Logique et théorie de la connaissance > Mathématiques

La trigonométrie

La trigonométrie '(du grec trigônon, triangle; metron, mesure) est une branche des mathématiques qui étudie les relations entre les côtés et les angles d'un triangle, les fonctions trigonométriques (fonctions circulaires), les relations entre ces fonctions, et leurs applications à différents problèmes. La trigonométrie a de nombreuses applications en physique, en navigation, en construction, etc. S'il s'agit de figures planes, composées de droites, on est dans le domaine de la trigonométrie rectiligne, tandis que la trigonométrie sphérique concerne les figures tracées à la surface d'une sphère et formées par des arcs de grands cercles. Comme un polygone quelconque (plan ou sphérique) peut se décomposer eu triangles, sa détermination complète se ramène à celle d'un triangle quelconque, ou plutôt à un enchaînement de triangles; c'est de là que vient le nom de trigonométrie.

Dans la division classiquement adoptée pour l'enseignement, la trigonométrie rectiligne ou euclidienne s'est constituée autour de trois chapitres distincts : études des fonctions circulaires; construction des tables trigonométriques; résolution des triangles. Une classification qui s'est avérée des plus fâcheuses et des moins logiques, comme le remarquait Laisant, il y a un siècle :

Les choses qu'on enseigne en trigonométrie sont très intéressantes et utiles, mais elles ne sont pas à leur place, et c'est souvent une cause de confusion dans les idées pour beaucoup de débutants. Il est certain, en effet, que l'étude des fonctions circulaires est du domaine de l'algèbre, bien que leur définition élémentaire rationnelle exige des considérations géométriques et une première notion des coordonnées. La construction des tables est une suite d'opérations de calcul qui relèvent de l'arithmétique. C'est à la troisième partie seule que devrait raisonnablement. appartenir le nom de trigonométrie. Ce vice d'organisation dans cette partie de l'enseignement provient, comme bien d'autres, du découpage excessif qu'on a voulu faire entre l'algèbre et la géométrie, et de la répugnance à introduire dans chaque science, dès le début, les idées utiles empruntées à une science voisine, même lorsqu'elles sont simples et qu'elles peuvent jeter une grande lumière sur le sujet, qu'on étudie. La notion des coordonnées, par exemple, la théorie des projections, devraient prendre place dans l'enseignement tout à fait élémentaire. (C.-A. Laisant).

Les concepts de la trigonométrie se sont révélés très tôt de la plus haute importance pour l'astronomie, la navigation, la géodésie, l'arpentage, etc.; aussi n'ont-ils pas attendu la définition de la trigonométrie en tant que discipline pédagogique pour avoir été l'objet de recherches étendues de la part des mathématiciens depuis très longtemps. C'est ainsi que Hipparque d'Alexandrie connaissait les solutions des cas les plus utiles de la trigonométrie sphérique, et l'on en trouve les formules fondamentales dans l'Analemme de Ptolémée. Cependant les Grecs, au lieu des sinus, employaient les cordes des arcs doubles. L'usage des sinus fut introduit par les Arabes, auxquels la science doit encore divers autres perfectionnements. Regiomontanus introduisit les tangentes, dont l'emploi a considérablement simplifié les calculs. Mais la forme élégante et concise qui distingue la trigonométrie actuelle est tout entière due aux immenses progrès de l'analyse moderne. (A19).

Approche géométrique

Relations entre les côtés et les angles d'un triangle plan

Résoudre un triangle, c'est en déterminer les parties inconnues, angIes, côtés, surface, à l'aide des parties données.

Un angle a pour mesure l'arc de cercle compris entre ses côtés, et décrit de son sommet comme centre avec un rayon quelconque. En trigonométrie, ou emploie indifféremment les mots arc et angle.

Il est difficile d'établir les relations qui existent entre les côtés d'un triangle et les arcs qui en mesurent les angles; aussi remplace-t-on dans les calculs la valeur des arcs par celle de certaines lignes qui en dépendent et dont la longueur varie avec la grandeur de ces arcs. Les arcs étant connus, ces lignes le sont aussi et réciproquement. Elles prennent le nom de lignes trigonométriques.

Ces lignes trigonométriques sont le sinus, la tangente, la sécante, le cosinus, la cotangente, la cosécante (d'autres pourraient être définies mais n'on pas d'intérêt pratique).

Relations trigonométriques dans un triangle rectangle.
Il convient de considérer d'abord un triangle rectangle dont l'un des deux angles aigus sera noté et dont les côtés sont notés : a (= côté adjacent ou base); b ( = côté opposé ou hauteur); c ( = hypothénuse).

Triangle rectangle.

Cosinus et sinus d'un angle.
On définit les sinus et les cosinus des angles aigus d'un triangle rectangle de la façon suivante :

• Le cosinus de l'angle a (noté cos a) est égal au rapport de la longueur du côté adjacent a à la longueur de l'hypoténuse c :
cos = a/c

• Le sinus de l'angle a (sin a) est égal au rapport de la longueur du côté opposé b à la longueur de l'hypoténuse c-:

sin = b/c

Tangente.
Alors que le cosinus et le sinus sont définis par rapport à l'hypothénuse du triangle, la tangente d'un angle aigu se définit par le rapport entre les deux autres côtés :

• La tangente de l'angle aigu a (tan a) est égale le rapport de la longueur du côté opposé b à la longueur du côté adjacent a :
tan = b/a, d'où : tan = sin / cos

Cotangente, sécante et cosécante.
On donnera encore les définitions suivantes :

• La cotangente est le quotient de la longueur du côté adjacent par la longueur du côté opposé :
cotan = a/bP, soit cotan = 1/ tan

• La sécante est le quotient de la longueur de l'hypothénuse par la longueur du côté adjacent :

sec = c/a, soit sec = 1/ cos

• La cosécante est le quotient de la longueur de l'hypothénuse par la longueur du côté opposé :

cosec = c/b, soit cosec = 1/sin

Remarque.
Les deux angles aigus d'un triangle rectangle étant complémentaires, il s'ensuit que le sinus, la tangente, la sécante de l'un sont le cosinus, la cotangente, la cosécante de l'autre.

Identités pythagoriciennes.
Les définitions du cosinus et du sinus permettent d'écrire : a = c.cos et b = c. sin . En appliquant le théorème de Pythagore, aura : c²cos² + c². sin² = c². Il suffit alors de diviser tous les termes par c² pour obtenir la relation qui existe entre le sinus et le cosinus d'un angle :

cos² + sin² = 1

Cette équation, dans laquelle on reconnaît aussi l'équation cartésienne du cercle unitaire, est aussi appelée relation fondamentale de la trigonométrie. C'est la première des relations dites identités pythagoriciennes. Les deux autres sont :

tan² +1 = sec²
1 +cot² = cosec²

(Elles s'obtiennent en divisant les termes de la première relation respectivement par cos²

et sin²

, puis en remplaçant les rapports ainsi obtenus par tan, sec, cot et cosec, d'après les définitions données plus haut. Il suffit ensuite de simplifier).

On voit que ces relations ne dépendent pas du triangle considéré.

Résolution d'un triangle quelconque.
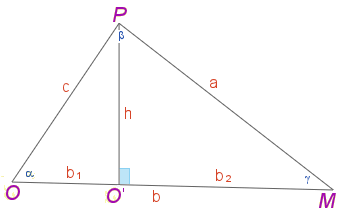
On considère maintenant un triangle quelconque OMP dont l'un des angles sera noté et dont les côtés adjacents sont notés : b et c; et le côté opposé a. L'angle peut être un angle aigu comme sur la figure ci-dessous ou un angle obtus si le point O se trouve sur le segment O'M. Dans le premier cas on a b2 = b- b1; dans le second cas, on aura : b2 = b + b1.

Triangle quelconque (loi des cosinus).

Lois des cosinus.
Dans la cas de la figure ci-dessus ( angle aigu), si l'on nomme h la hauteur de ce triangle, on pourra écrire en appliquant le théorème de Pythagore :

a² = h² + (b - b1)² et c² = h² + b1²

d'où, par soustraction de la seconde équation à la première :

a² - c² = (b - b1)² - b1²

On ajoute c² aux deux membres de l'équation et on développe (b - b1)² :

a² = c² + b² - 2bb1 + b1²- b1²

Soit :

a² = c² + b² - 2bb1

OO'P étant un triangle rectangle, on a : b1 = c.cos . Il s'ensuit que :

a² = b² + c² - 2bc.cos

Le même résultat serait obtenu avec

angle obtus. Et si l'on

l'angle dont le sommet est P et

celui dont le sommet est M, on obtient par permutation circulaire :

b² = a² + c² - 2ac.cos
et
c² = a²+b² - 2ab.cos

Ces trois équations résument le théorème (ou loi) des cosinus, aussi appelé théorème d'Al-Kashi, ou encore ou théorème de Pythagore généralisé.

Loi des sinus.
La figure ci-dessous reproduit la précédente, mais en y ajoutant le segment k, perpendiculaire au segment c, formant donc un nouveau triangle rectangle dont le sommet N correspond à l'angle droit.

Triangle quelconque (loi des sinus).

Par définition du sinus on a : sin = h/c et sin = h/ a d'où : h = c. sin = a. sin ou encore :

a/sin = c/sin .

De même, on peut écrire : sin

= k/a et sin

= k/b, d'où k = b. sin

= b. sin

,
ou encore :

a/sin = b/sin

Il s'ensuit donc que :

a/sin = b/sin = c/sin

Autrement dit, les longueurs des côtés d'un triangle sont proportionnelles aux sinus des angles opposés. C'est la loi des sinus.

Cercle, triangles et lignes trigonométriques
Soit un cercle de rayon R = 1 (rayon égal à l'unité linéaire), et deux de ses diamètres perpendiculaires entre eux AA' et BB'. Soit de plus un angle quelconque AOP. L'arc AP que nous appellerons est la mesure de l'angle AOP. Les segments PM, AT, sont menées perpendiculairement au diamètre AA'; BS et PN, perpendiculairement au diamètre BB'. Plusieurs triangles rectangles, dont les côtés sont nommés lignes trigonométriques, ont ainsi été construits :

Cercle trigonométrique.

Cercle et lignes trigonométriques.

Sinus et cosinus.
Le triangle OMP permet de définir le sinus et le cosinus.

• Le sinus d'un arc a, selon la définition donnée plus haut, est égal au rapport de la longueur du côté opposé (ici noté PM) à la longueur de l'hypoténuse (OP). Or comme le rayon du cercle considéré est égal à 1 (OP = 1), il s'ensuit que sin = PM. Autrement dit, le sinus d'un arc est la perpendiculaire abaissée de l'extrémité de l'arc sur le diamètre passant par l'origine de cet arc.
• Le cosinus d'un arc, de la même façon, peut alors se définir comme la partie du rayon comprise entre le centre du cercle et le pied du sinus. On a cos = OM = NP.

Le cosinus de l'arc AP est OM et le sinus de l'arc BP est NP. Comme OM = NP, il s'ensuit que le cosinus d'un arc est égal au sinus de son complément.

Tangente et sécante.
Le triangle OAT permet de définir la tangente et la sécante.

• La tangente, selon la définition donnée plus haut, est égale au rapport de la longueur du côté opposé (ici noté AT) à la longueur du côté adjacent (OA). Comme la longueur du côté adjacent est égale à 1, tan = AT. On peut dès lors donner le nom de tangente au segment de droite mené tangentiellement à l'arc depuis son origine A jusqu'au prolongement T du rayon passant par l'extrémité de cet arc.
• La sécante, enfin, et partant du même raisonnement, peut être définie comme le segment de droite qui va du centre O à l'extrémité T de la tangente. On a donc sec = OT.

Cotangente et cosécante.
Le triangle OSB permet de définir la cotangente et la cosécante. Il suffit de remarquer que l'angle formé par les segments SB et SO est égal à l'angle

. AT/OA = OB/BS, et puisque OA = OB = 1 : AT =1/BS ou BS = 1/AT, soit donc BS = 1/ tan

. C'est, comme on l'a vu la définition de la cotangente :

• La cotangente est la longueur du segment de droite menée tangentiellement à l'arc depuis I'origine de son complément jusqu'à la rencontre du prolongement du rayon passant par l'extrémité de l'arc. On a cotan = BS.
• La cosécante, en raisonnant de la même manier peut se définir comme la longueur du segment de droite qui va du centre à l'extrémité de la cotangente. On a cosec = OS.

Trigonométrie sphérique

De la même façon que la trigonométrie euclidienne s'occupe de la résolution des triangles dans le plan, la trigonométrie sphérique s'occupe de la résolution des triangles sphériques, c'est-à-dire des triangles tracés sur la surface de la sphère. Il existe ainsi des analagies entre ces deux parties de la géométrie, mais aussi des différences.

Les triangles sphériques.
La première différence à considérer est celle qui distingue les triangles sphériques et les triangles plans.

• Dans un triangle sphérique, les côtés ne sont plus des segments de droites, mais des arcs de grands cercles tracés sur la sphère.
• Ces arcs étant mesurés par l'angle au centre (de la sphère) qui les définit, on n'a plus à considérer ici que des angles, alors que dans le plan, il s'agissait de considérer des angles et des longueurs.
• Il s'ensuit que dans un triangle sphérique les sinus, cosinus, tangentes, etc. peuvent être définis non seulement pour les angles aux sommets, mais aussi pour les côtés.
• Dans un triangle sphérique, la mesure de la somme des angles aux sommets est supérieure à celle de deux angles droits et inférieure à celle de 6 angles droits : radians (180°) < < 3. radians (540°).
• Il existe des triangles sphériques dont les trois angles sont rectangles (la somme de la mesure des angles est alors égale celle de 3 droits, soit 270° ou 3/2. radians).
Les angles aigus ou obtus d'un angle sphérique sont appelés angles obliques. Lorsqu'un triangle sphérique n'a qu'un seul angle droit, le côté opposé s'appelle hypothénuse.

Triangle sphérique.

Résolution des triangles sphériques.
On désignera ici les angles aux sommets des triangles sphériques par des lettres majuscules (A, B, C). Les arcs qui forment les côtés opposés respectifs seront désignés par des lettres minuscules (a, b, c).

Donnons les principaux résultats de la trigonométrie sphérique.

Loi des cosinus.

cos a = cos b .cos c + sin b .sin c .cos A
cos A = -cos B .cos C + sin C .sin C .cos a

(Les cosinus des autres angles s'obtiennent par des permutations circulaires).

Loi des sinus.

sin A / sin a = sin B / sin b = sin C / sin c

Tangentes.
Posons : s = (a + b + c)/2 et S = (A +B + C)/2. On aura alors :

tan² (A/2) = sin(s–b). sin(s–c) / sin s.sin(s–a)
tan² (a /2) = -cos(S). cos(S-A) / cos(S-B). cos(S-B)

Ces formules permettent de calculer l'angle au sommet quand on connaît les côtés ou, à l'inverse de calaculer les les côtés à partir d'un angle au sommet connu.

Cas des triangles rectangles.
Supposons que C est un angle droit.

sin a = sin A. sin c = tan b. cotan B
sin b = sin B. sin c = tan a. cotan A
cos c = cotan A .cot B = cos a .cos b
cos A = cos a .sin B = tan b. cotan c
cos B = cos b. sin A = tan a .cotan c

Approche analytique

Fonctions circulaires

Le cercle trigonométrique.
On appelle cercle trigonométrique un cercle de centre O et de rayon 1, pour lequel sont définis un axe Ox et un axe Oy perpendiculaire (repère orthonormé), ainsi qu'un sens sens de parcours de ce cercle (sens inverse de celui du déplacement des aiguilles d'une montre) choisi pour sens positif.

Cercle trigonométrique.

A chaque nombre réel x on fait correspondre un point P du cercle trigonométrique. P étant le point tel que l'angle orienté de Ox avec le vecteur OP ait une mesure en radians égale à x.

Fonctions cosinus, sinus et tangente.
Par définition, on appelle :

• Le cosinus du nombre réel x la mesure algébrique de la projection sur Ox du vecteur OP; on peut aussi définir cos x comme l'abscisse du point P dans le repère OxOy.
• Le sinus du nombre réel x la mesure algébrique de la projection sur Oy du vecteur OP; on peut aussi dire que sin x est l'ordonnée du point P.
• La tangente du nombre x est définie comme étant le rapport de sin x à cos-x :

tan x = sin x / cos x

Note : Pour alléger l'écriture, on omet ordinairement les parenthèses lorsqu'il n'y a pas de risque de confusion; en toute rigueur on devrait écrire : tan(x), sin(x), cos (x), etc.

Propriétés analytiques des fonctions circulaires.
Propriétés des fonctions sinus et cosinus.
Les fonctions sinus et cosinus sont définies pour tout x réel. Les valeurs qu'elles prennent appartiennent à l'intervalle réel [ -1, +1];

Elles sont continues et périodiques, de période 2, c'est-à-dire que lorsque x augmente ou diminue d'un multiple entier de 2les fonctions circulaires reprennent la même valeur.

sin (x + 2 k) = sin x (où k )
cos (x + 2k) = cos x

La fonction cosinus est paire : cos x = cos -x; la fonction sinus est impaire : -sin x = sin -x.

Ce sont des fonctions dérivables sur . La dérivée de la fonction cosinus est l'opposé de la fonction sinus :

(cos x)' = - sin x

La dérivée de la fonction sinus est la fonction cosinus :

(sin x)' = cos x

Le tableau suivant résume les variations des fonctions sinus et cosinus dans l'intervalle [0, 2

]. Les valeurs prises par ces fonctions évoluent entre +1 et -1.

x	0---------/2-------------------3/2------ -2
y = sin x	0-------1------- 0---------1---------0
y = cos x	1------- 0 --------1---- ---- 0---------1

Leurs courbes représentatives sont appelées sinusoïdes :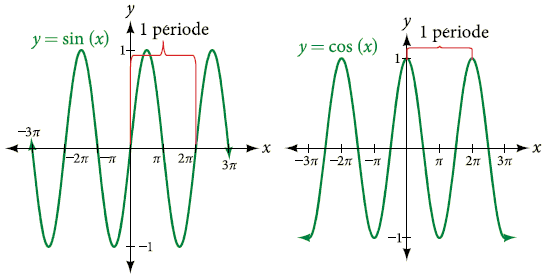

Sinusoïdes (représentations graphiques des fonctions sinus et cosinus).

Propriétés des fonctions tangente et cotangente.
La fonction tangente est définie pour tout x appartenant à - {/2 - k}; la fonction cotangente x - {k}; dans les deux cas k .

Les fonctions tangente et cotangente ont pour période :

tan (x + k) = tan x (où k )
cotan (x + k) = cotan x

Il suffit dès lors d'étudier leur variation dans un intervalle égal à

; prenons l'intervalle ]-

/2, +

/2[. Quand x croît dans cet intervalle, tan x croît dans l'intervalle ]-

, +

[. Et puisque cotan x = 1/ tan x, cotan x varie en sens inverse de tan x. On peut établir établir de tableau suivant :

x	-/2-----------0---------------/2
y = tan x	----------- 0------------+
y = cotan x	0------- \| +--------- 0

On voit que tan x et cotan x peuvent prendre toutes les valeurs de - 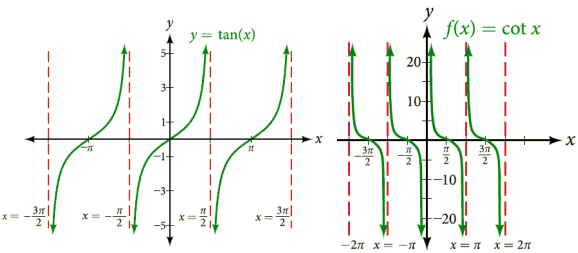à +. De plus, y = tan x n'est pas définie pour x = /2 + k ; y = cotan x, pour x = k (avec k ).

Représentations graphique sdes fonction tangente et cotangente.

La dérivée de y = tan x est y' = 1/cos² x; celle de y = cotan x est y' = -1/sin² x.

Relations entre les différentes fonctions circulaires.

sin² x + cos² x = 1
1 + tan² x = 1/cos² x
1+ cotan² x = 1/sin² x

On retrouve donc des relations déjà vues en géométrie, la différence qu'on ne parle plus de l'angle

, mais du nombre réel x. Et, de la même façon qu'on avait remarqué à propos des relations pythagoriciennes, qu'elles s'affranchissaient de la notion même de triangle, on peut souligner maintenant les fonctions circulaires peuvent s'envisager indépendamment de tout concept géométrique.

Formules d'addition.

cos (a + b) = (cos a.cos b) - (sin a.sin b)
sin (a+ b) = (sin a.cos b + (sin b.cos a)
tan (a + b) = (tan a + tan b) / (1 - tan a. tan b)
cos (a-b) = (cos a.cos b) + (sin a.sin b)
sin (a-b) = (sin a.cos b) - (sin b.cos a)
tan (a - b) = (tan a - tan b) / (1 + tan a. tan b)

Si l'on note t = tan a/2 :

cos a = (1-t²) / (1+t²)
sin a = 2t / (1 + t²)
tan a = 2t / (1 - t²)

Formules de transformation de sommes en produits.

cos a + cos b = 2 . cos (a+b) / 2 . cos (a-b) / 2
sin a + sin b = 2 . sin (a+b)/2 . sin (a-b) / 2
cos a - cos b = - 2 . sin (a+b) / 2 . cos (a-b) / 2
sin a - sin b = 2 . sin (a-b)/2 . cos (a+b) / 2
tan a + tan b = [sin (a+b)] / [cos a. cos b]
tan a - tan b = [sin (a-b)] / [cos a. cos b]

Sécante, cosécante et tangente.
On a vu plus haut qu'on a donné des noms particuliers à l'inverse du cosinus du sinus et de la tangente. On notera donc simplement ici que :

• La sécante (sec) est une fonction périodique définie comme :
sec x = 1/cos x

• La cosécante (cosec) est une fonction périodique définie comme :

cosec x = 1/sin x

• La cotangente (cotan) est la fonction définie comme :
cotan x = 1/ tan x

Remarque.
Le cosinus, la cotangente et la cosécante d'un arc n'étant que le sinus, la tangente et la sécante du complément de cet arc sont appelés pour cette raison fonctions complémentaires.

Fonctions circulaires réciproques.
La notion de fonction réciproque répond qu'à l'image d'une fonction on peut associer par une autre fonction (la fonction réciproque) l'antécédent de cette image. Pour qu'une fonction ait une réciproque, il faut que cette fonction soit bijective (toute image a un antécédent unique). Les fonctions trigonométriques sinus, cosinus, sécante et cosécante ne sont sont pas bijectives, car elle ne sont pas injectives (par exemple une infinité de valeurs de x (x) correspondent à l'égalité cos x = b, b [-1,1] : x , x+2, x+4,..., x+2n,...). Il est cependant possible de restreindre le domaine de définition de ces fonctions pour que sur l'intervalle considéré la fonction soit bijective. Les fonctions trigonométriques inverses peuvent alors être définies :

• L'arc sinus d'un réel x (x [-1,1]) est le réel y (y [-/2, /2]) dont le sinus est x : y = arcsin x.
• L'arc cosinus d'un réel x (x [-1,1]) est le réel y (y [0, ]) dont le cosinus est x : y = arccos x.
• L'arc tangente d'un réel x (x ) est le réel y (y [-/2, /2]) dont la tangente est x : y = arctan x.
• L'arc cotangente d'un réel x (x ) est le réel y (y [0, ]) dont la cotangente est x : y = arccotan x.
• L'arc sécante d'un réel x (x ]-,-1 ]U [1,+[) est le réel y
(y [0, /2[ U ] /2, ]) dont la cotangente est x : y = arcsec x.
• L'arc cosécante d'un réel x (x ]-,-1]U[1,+[) est le réel y
(y [-/2, 0[ U ] 0, /2]) dont la cotangente est x : y = arccsec x.

Fonctions circulaires et exponentielle.
Sinus, cosinus et nombres complexes.
Les éléments de

(corps des nombres complexes) peuvent s'écrire sous la forme : z-= a+i.b, où est tel que i² = -1. Si le point image de z appartient au cercle trigonométrique, z est un nombre complexe de module 1 et on a :

z = cos x + i.sin x

C'est une formulation qui peut déjà simplifier bien des calculs (par exemple en s'aidant de la formule de Moivre : (cos x + i.sin x)ⁿ = cos nx + i.sin nx, pour tout n entier relatif), mais dont l'intérêt apparaît pleinement quand on rapproche les fonctions sinus et cosinus de la fonction exponentielle à variable imaginaire pure e^ix, où e = 2,718281828... est le nombre d'Euler, base des logarithmes naturels.

Développements en série de sin, cos et e^ix.
On comprend intuitivement que la valeur à proximité d'un point x d'une fonction continue et indéfiniment dérivable peut se calculer à partir de la valeur de la fonction et de sa dérivée en ce même point. La dérivée correspond à la pente en ce point et permet de calculer la quantité qu'il faut ajouter (ou soustraire) à la valeur de la fonction pour connaître sa valeur en un point proche.

Un enchaînement de plusieurs théorèmes généraux (théorème de Rolle, théorème des accroissements finis, théorèmes de Taylor et Mac laurin) aboutit à exprimer toute fonction (ayant les propriétés de continuité et de dérivabilité requises) comme la somme (appelée développement en série) de quantités de plus en plus petites, calculées à partir de la valeur de la fonction et et de sa dérivée en un point. La formule dite de Mac Laurin est un des expressions possible. Dans le cas des fonction sinus et cosinus, dont les dérivées respectives, on l'a vu, sont (cos x)' = - sin x et (sin x)' = cos x :

Le point d'exclamation "!" indique une factorielle : n! = 1.2.3... (n-1).n

La formule de Mac Laurin appliquée maintenant à la fonction exponentielle à variable imaginaire e^ix , qui est sa propre dérivée, correspond au développement en série suivant :

On voit que lorsqu'on regroupe les termes de rang pair d'une part et ceux de rang impair de l'autre, on obtient :

e^ix = cos x + i. sin x (formule d'Euler)

L'exponentielle révèle ainsi ses liens avec des fonctions qui ont leur origine dans la géométrie du triangle, tandis que les fonctions cosinus et sinus (et les autres fonctions circulaires) s'avèrent pouvoir être définies à partir de la seule fonction exponentielle :

cos x = (e^ix + e^-ix ) / 2
sin x = (e^ix- e^-ix) / 2i

Cette profonde unité des mathématiques, si propre à susciter l'étonnement et même l'émotion esthétique, apparaît d'une manière encore plus remarquable lorsque, dans la formule d'Euler, on pose x =

Comme cos

= -1 et sin

= 0; on a :

Pour faire apparaître plus clairement les constantes mathématiques (e, i,

, 1, 0) et les opérations arithmétiques (+, x, ^) impliquées , cette équation, appelée identité d'Euler, peut aussi écrire sous sa forme canonique :

Fonctions hyperboliques

On peut définir les fonctions hyperboliques par analogie avec les fonctions circulaires sur la base de leurs définitions à partir de l'exponentielle. Ainsi ne considère-t-on plus la quantité imaginaire pure ix, mais la quantité complexe x, telle que x = a + ib, pour poser les relations qui définissent le cosinus (cosh) et le sinus (sinh) hyperboliques :

cosh x = (e^x + e^-x ) / 2
sinh x = (e^x- e^-x) / 2

L'analogie peut être poursuivie pour définir les fonctions tangente hyperbolique (tanh), cotangente hyperbolique (cotanh), etc. :

tanh x = sinh x/ cosh x
cotanh x = 1/tanh x
sech x = 1/cosh x
cosech x = 1/sinh x

Comme on peut s'y attendre, les relations déjà mentionnées dans le cas des fonctions circulaires, ont leur équivalent avec les fonctions hyperboliques. Mentionnons seulement pour exemples :

cosh (a + b) = (cosh a . cosh b) - (sinh a . sinh b)
sinh (a + b) = (sinh a . sinh b) + (cosh a . cosh b)
tanh (a + b) = (tanh a + tanh b) / (1 + tanh a . tanh b)

Quant à la première identité pythagoricienne, elle a pour pour analogue :

cosh² x - sinh² x = 1

On reconnaît là l'équation d'une hyperbole et l'on comprend au passage le qualificatif d'hyperboliques donné aux fonctions considérées ici. L'hyperbole joue dans la trigonométrie hyperbolique le même rôle que le cercle dans la trigonométrie circulaire.

La formule d'Euler devient :

e^x = cosh x + sinh x ou e^(a+ib) = cosh (a+ib) + sinh (a+ib)

Dictionnaire Idées et méthodes