 |
On
nomme ensemble toute collection, réunion ou classe d'objets. Ces
objets sont appelés éléments. Les notions d'ensemble et
d'élément ne peuvent pas recevoir de véritable définition. Mais
des correspondances qui permettent de les caractériser peuvent être établies
entre ensembles, entre éléments, et entre éléments et ensembles. Selon
les objets concernés et les caractères des correspondances, on parlera
pour les désigner de relations, d'applications ou de lois de composition.
Toutes les mathématiques pourraient ainsi être définies comme l'étude
des ensembles des éléments et de leurs relations.
Ainsi définit-on
entre les éléments et l'ensemble la relation d'appartenance.
De
même entre les ensembles définit-on une relation d'inclusion. On peut
aussi définir la réunion de deux ensembles qui correspond à l'ensemble
dont les éléments appartiennent à l'un ou à l'autre des des
ensembles réunis, et l'intersection de deux ensembles qui est l'ensemble
composé des éléments appartenant à la fois à l'un et
à l'autre ensemble.
La théorie des
ensembles initiée par Georg Cantor (1845-1918)
dès les années 1870 a été reformulée et axiomatisée ensuite de diverses
façons, à partir du début du XXe siècle,
par des mathématiciens tels qu'Ernst Zermelo (1871-1953), Abraham Fraenkel
(1891-1965), Thoralf Skolem (1887-1963) et d'autres ( Histoire
des mathématiques). C'est une théorie qui questionne les fondements
des mathématiques et, à ce titre, se hérisse de grandes difficultés
dans lesquelles on ne saurait entrer ici. On se contentera donc seulement
dans cette page d'initiation d'introduire, sans chercher la rigueur qu'un
exposé mathématique même élémentaire aurait exigé, le vocabulaire
produit par cette théorie. C'est aujourd'hui le vocabulaire de base de
toutes les mathématiques. Il est même utilisé bien-delà des mathématiques,
chaque fois qu'il convient de formaliser un concept. Histoire
des mathématiques). C'est une théorie qui questionne les fondements
des mathématiques et, à ce titre, se hérisse de grandes difficultés
dans lesquelles on ne saurait entrer ici. On se contentera donc seulement
dans cette page d'initiation d'introduire, sans chercher la rigueur qu'un
exposé mathématique même élémentaire aurait exigé, le vocabulaire
produit par cette théorie. C'est aujourd'hui le vocabulaire de base de
toutes les mathématiques. Il est même utilisé bien-delà des mathématiques,
chaque fois qu'il convient de formaliser un concept.
Ensembles et éléments
On convient de représenter
les ensembles par des lettres majuscules : A, B, C, D, E, etc., et les
éléments des ensembles sont représentés par des lettres minuscules
: a, b, c, d, e, etc.
Connecteurs
logiques, quantificateurs.
La théorie des
ensembles utilise par ailleurs un certain nombre de notions et de signes
venus de la logique symbolique :
‚ÄĘ On utilise
le signe = entre deux ensembles A et B lorsque tout ce qui peut être dit
de A peut être dit de B (et donc que tout ce qui peut être dit de B peut
être dit de A). A = B signifie que deux ensembles sont égaux, c'est-à-dire
identiques. Le même signe = s'utilise pour signifier l'égalité de deux
éléments. Pour signifier qu'il n'y a pas d'égalité on utilise le signe 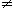 (A
(A 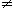 B se
lit "A est différent de B"). Mais le signe égal a aussi d'autres utilisations
: il sert à définir un ensemble, a exprimer sa notation, etc. B se
lit "A est différent de B"). Mais le signe égal a aussi d'autres utilisations
: il sert à définir un ensemble, a exprimer sa notation, etc.
‚ÄĘ Un √©nonc√©
dont on peut dire s'il est vrai ou faux est appelé une proposition (notons-là
P).
Quand une proposition est vraie, on pourra dire que la condition qu'elle
énonce est satisfaite ou remplie.
‚ÄĘ Lorsque le fait
qu'une proposition P soit vraie entra√ģne que la proposition
Q
est également vraie on écrit P'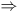 Q ("P implique Q"). Si, de plus Q'
Q ("P implique Q"). Si, de plus Q'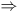 'P,
on pourra écrire P 'P,
on pourra écrire P 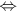 Q ("P est équivalent à Q).
Q ("P est équivalent à Q).
‚ÄĘ La barre verticale
| (ou oblique /) signifie "tel que", et fait le lien entre deux termes,
le premier étant un élément, le second une condition statisfaite. Ainsi
lorsqu'on écrit : x | P (ou x / P), on signifie que l'élément
"x est tel que la proposition P est vraie", que "x est est tel que
la condition P est remplie", ou même encore que "x possède la
propriété P".
‚ÄĘ Le quantificateur
universel  se lit "pour tout
", "quel que soit", et s'applique à un terme ( se lit "pour tout
", "quel que soit", et s'applique à un terme ( x) ou à une série de termes (
x) ou à une série de termes ( x, y, z, etc.). On utilise les deux points " : " pour associer une propriété
au terme ainsi quantifié. Par exemple, "
x, y, z, etc.). On utilise les deux points " : " pour associer une propriété
au terme ainsi quantifié. Par exemple, " x : x = y" se lira "pour tout x on a x égal à x".
x : x = y" se lira "pour tout x on a x égal à x".
‚ÄĘ Le quantificateur
universel 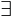 se lit "il existe".
Pour dire "il n'existe pas", "aucun", on écrira" ~ se lit "il existe".
Pour dire "il n'existe pas", "aucun", on écrira" ~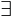 "
ou "
ou 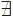 . L'écriture . L'écriture 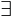 !
signifie quant à elle : "il existe un et un seul". !
signifie quant à elle : "il existe un et un seul".
Définition
par extension et par compréhension.
Un ensemble peut
être défini de plusieurs façons selon qu'on en énumère tous les éléments,
ou qu'on énonce une propriété commune et univoque de tous ses
éléments.
‚ÄĘ D√©finition
d'un ensemble en extension. - Lorsqu'un ensemble est déterminé en en
donnant le liste des éléments qui le composent, on dit qu'il est défini
en
extension. Dans ce cas, on écrit les éléments de la liste entre
accolades {}, chaque élément étant séparé par une virgule. Ainsi,
l'ensemble E = {a, b, c, d, e, f} est-il donné en extension. L'ordre dans
lequel sont listés les éléments est sans importance : {a, b, c} = {c,
a, b}. (Notez au passage les significations différentes que nous faisons
dans ces deux exemples du signe =, dans le premier, il est seulement une
abréviation qui signifie "est le nom de l'ensemble", dans le second
cas, il s'agit du symbole logique qui marque l'égalité ou l'identité
entre deux termes).
‚ÄĘ D√©finition d'un
ensemble en compréhension. - Lorqu'un ensemble est déterminé au moyen
d'une propriété caractéristique ou d'une condition, qui est commune
à tous les éléments de l'ensemble, on dit qu'il est défini en compréhension.
Par exemple l'ensemble F est donné en compréhension lorsqu'on écrit
: F = {x / x est impair }. Ce que l'on peut lire : "F est (le nom de) l'ensemble
des nombres x, tels que x un nombre impair".
On dit qu'un ensemble
est bien défini lorsque l'on peut en identifier tous les éléments.
C'est-à-dire que, pour un objet donné, il est toujours possible de dire
s'il est ou s'il n'est pas un élément de l'ensemble.
Représentation
graphique des ensembles.
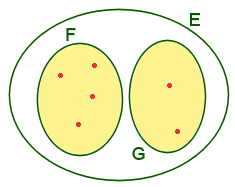
Les diagrammes
de Venn offrent une manière commode de représenter les ensembles
et leurs éléments. Dans un diagramme de Venn (1834-1923) une ensemble
est représenté par une courbe fermée; ses éléments y sont figurés
par des points placés à l'intérieur de l'espace circonscrit par cette
courbe.
-
Diagramme
de Venn
de
l'ensemble E = {a, b, c}.
On rencontre aussi
une représentation graphique des ensembles très similaire à celle de
Venn, c'est celle d'Euler. On en a donné un exemple
plus bas avec le schéma représentant une partition. Dans ce diagramme
d'Euler les deux courbes fermées représentant des ensembles distincts
sont disjointes; dans un un diagramme de Venn, les deux courbes fermées
se seraient entrecoupées, et leur intersection aurait correspondu à l'ensemble
vide. Pour éviter d'avoir à choisir entre l'une ou l'autre de ces représentations,
on parle souvent diagrammes de Venn-Euler.
Quoi qu'il en soit,
de tels diagrammes, comme toute figure en général que l'on peut rencontrer
dans un exposé mathématiques sont des outils pour "voir les choses",
pour comprendre intuitivement une situation, mais on ne peut en aucune
façon en faire des outils de démonstration.
Ensembles vide,
unitaire, fini, infini
Ensemble
vide.
Parmi tous les ensembles,
on peut en définir un qui ne contient aucun élément : c'est l'ensemble
vide. Il est noté : 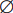 ou {-}. Notez
que {
ou {-}. Notez
que { 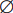 } n'est pas l'ensemble vide : c'est l'ensemble qui contient l'ensemble
vide; il contient donc un élément.
} n'est pas l'ensemble vide : c'est l'ensemble qui contient l'ensemble
vide; il contient donc un élément.
Singleton.
Un ensemble qui
ne contient qu'un seul élément est qualifié d'ensemble unitaire
ou, plus couramment de singleton. Par exemple {-x-}
est le singleton dont l'élément est x.
Ensemble
fini. Ensemble infini.
Un ensemble fini
est un ensemble dont on peut compter les éléments, et dont on peut donc,
en principe, donner la liste complète, c'est-à-dire un ensemble qui peut
être défini en extension.
Un ensemble infini
est un ensemble pour lequel ce comptage n'est pas possible. Il peut arriver,
cependant, dans certains cas, qu'à chaque élément d'un ensemble infini
il soit possible d'attacher une nombre entier (un peu comme une étiquette).
On dit alors que cet ensemble dénombrable. Un ensemble infini dénombrable
est un ensemble dont tout élément x peut, par exemple, être doté d'un
indice : x1, x2, x3,
etc. Tous les ensembles fini sont dénombrables.
Appartenance et
d'inclusion.
Eléments,
appartenance.
La première des
correspondances qui peut être établie entre un élément
e et
un ensemble E est son appartenance ou non à cet ensemble. L'appartenance
est notée  ; ainsi, e ; ainsi, e  E signifie-t-il que "l'élément e appartient à l'ensemble E".
Pour signifier que e n'appartient pas à E on écrira e
E signifie-t-il que "l'élément e appartient à l'ensemble E".
Pour signifier que e n'appartient pas à E on écrira e  E.
E.
 Du
fait même des postulats de la théorie des ensembles, tout élément
appartient à un ensemble : Du
fait même des postulats de la théorie des ensembles, tout élément
appartient à un ensemble :  x : x
x : x  {x}. {x}.
 La
relation d'appartenance n'autorise pas non plus la mise en correspondance
de deux ensembles : un ensemble ne peut pas appartenir à un autre ensemble
(et, a fortiori, un ensemble ne peut pas être un élément de lui-même).
Ainsi, par exemple, ne pourra-t-on pas écrire E La
relation d'appartenance n'autorise pas non plus la mise en correspondance
de deux ensembles : un ensemble ne peut pas appartenir à un autre ensemble
(et, a fortiori, un ensemble ne peut pas être un élément de lui-même).
Ainsi, par exemple, ne pourra-t-on pas écrire E  F; en revanche si F = {E}, autrement dit si F est l'ensemble dont E est
l'élément, on pourra avoir E
F; en revanche si F = {E}, autrement dit si F est l'ensemble dont E est
l'élément, on pourra avoir E  {E}.
{E}.
Sous-ensembles,
inclusion.
Lorsque tous les
éléments d'un ensemble F appartiennent aussi à une ensemble E, on dit
que "l'ensemble F est inclus dans l'ensemble E" ou que "F est un sous-ensemble
(ou une partie) de E", et l'on écrit : F 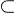 E.
E.
-
Inclusion.
-
Si l'on veut être plus
précis, on est conduit à distinguer le cas de l'inclusion stricte
(symbole  ),
o√Ļ tous les √©l√©ments de E appartiennent √† F, mais sans que tous les
√©l√©ments de F appartiennent √† E (le cas, donc, o√Ļ E est diff√©rent
de F) et le cas de l'inclusion au sens large (symbole ),
o√Ļ tous les √©l√©ments de E appartiennent √† F, mais sans que tous les
√©l√©ments de F appartiennent √† E (le cas, donc, o√Ļ E est diff√©rent
de F) et le cas de l'inclusion au sens large (symbole  )
qui correspond √† la situation o√Ļ E )
qui correspond √† la situation o√Ļ E 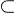 F ou E = F. Dans la pratique on ne fait pas cette distinction et on utilise
seulement le symbole
F ou E = F. Dans la pratique on ne fait pas cette distinction et on utilise
seulement le symbole 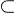 en l'entendant comme symbole de l'inclusion au sens large.
en l'entendant comme symbole de l'inclusion au sens large.
 Axiome
d'extension : dans la théorie des ensembles, on appelle ainsi l'énoncé
suivant : "deux ensembles E et F sont égaux si et seulement si ils possèdent
les mêmes éléments". On peut aussi dire " L'ensemble E est égal à
l'ensemble F si et seulement si E est inclus dans F et F est inclus dans
E", et de façon plus formelle : E = F Axiome
d'extension : dans la théorie des ensembles, on appelle ainsi l'énoncé
suivant : "deux ensembles E et F sont égaux si et seulement si ils possèdent
les mêmes éléments". On peut aussi dire " L'ensemble E est égal à
l'ensemble F si et seulement si E est inclus dans F et F est inclus dans
E", et de façon plus formelle : E = F 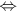 [E
[E 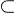 F
et F F
et F E]. E].
 Les
sous-ensembles (ou parties) d'un ensemble E sont des ensembles. Mais il
peut être utile de les considérer aussi comme des éléments d'un ensemble.
Cet ensemble - l'ensemble des parties de E donc - est noté Les
sous-ensembles (ou parties) d'un ensemble E sont des ensembles. Mais il
peut être utile de les considérer aussi comme des éléments d'un ensemble.
Cet ensemble - l'ensemble des parties de E donc - est noté  (E).
Il a en particulier pour éléments E lui-même et l'ensemble vide' (E).
Il a en particulier pour éléments E lui-même et l'ensemble vide'  .
Et on peut montrer que si E possède a éléments .
Et on peut montrer que si E possède a éléments  (E)
en possède 2ª. (Cette remarque conduit à une autre convention d'écriture
pour l'ensemble des parties de E : (E)
en possède 2ª. (Cette remarque conduit à une autre convention d'écriture
pour l'ensemble des parties de E : 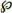 (E)
= 2E, qui est aussi appelé l'ensemble
puissance de E). (E)
= 2E, qui est aussi appelé l'ensemble
puissance de E).
 Un
ensemble de parties (ou de sous-ensembles) de E est aussi appelé une famille
de parties (ou de sous-ensembles) de E. Un
ensemble de parties (ou de sous-ensembles) de E est aussi appelé une famille
de parties (ou de sous-ensembles) de E.
 La
relation d'inclusion n'autorise pas la mise en correspondance d'un élément
avec un ensemble (un élément ne peut pas être inclus dans un ensemble).
Ainsi, par exemple, ne pourra-t-on pas écrire e La
relation d'inclusion n'autorise pas la mise en correspondance d'un élément
avec un ensemble (un élément ne peut pas être inclus dans un ensemble).
Ainsi, par exemple, ne pourra-t-on pas écrire e 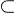 E; en revanche si F = {e}, autrement dit si F est l'ensemble dont e est
l'élément, on pourra éventuellement avoir F
E; en revanche si F = {e}, autrement dit si F est l'ensemble dont e est
l'élément, on pourra éventuellement avoir F 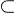 E, soit {e}
E, soit {e} 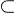 E.
E.
 La
théorie des ensembles ne permet pas de parler en un sens absolu de l'ensemble
de tous les ensembles sans s'exposer à un paradoxe. Mais il peut
être nécessaire de recourir à la notion d'ensemble de tous les ensembles
sur
lesquels on travaille : on désigne alors cet ensemble sous le nom
d'ensemble universel, d'univers, ou de référentiel. La
théorie des ensembles ne permet pas de parler en un sens absolu de l'ensemble
de tous les ensembles sans s'exposer à un paradoxe. Mais il peut
être nécessaire de recourir à la notion d'ensemble de tous les ensembles
sur
lesquels on travaille : on désigne alors cet ensemble sous le nom
d'ensemble universel, d'univers, ou de référentiel.
Intersection, réunion.
Intersection
de deux ensembles.
Il peut arriver
que deux ensembles E et F possèdent certains de leurs éléments en commun.
L'ensemble G constitué de ces éléments est appelé l'intersection
de E et de F : on notera G = E  F, et on lira "G égale E inter F".
F, et on lira "G égale E inter F".
-
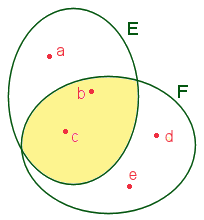
Intersection
G des ensembles E et F.
E
= {a, b, c}, F = {b, c, d, e}
G
= {b, c}.
 L'ensemble
G est inclus dans l'ensemble E (c'est un sous-enesmble de E) et il est
inclus dans l'ensemble F(c'est un sous-ensemble de F) : G L'ensemble
G est inclus dans l'ensemble E (c'est un sous-enesmble de E) et il est
inclus dans l'ensemble F(c'est un sous-ensemble de F) : G  E et G'
E et G'  F.
F.
 Si
les deux ensembles E et F n'aucun élément en commun, on dit qu'ils sont
disjoints.
Leur intersection est égale à l'ensemble vide :
E Si
les deux ensembles E et F n'aucun élément en commun, on dit qu'ils sont
disjoints.
Leur intersection est égale à l'ensemble vide :
E  F = F =  . .
Réunion
de deux ensembles.
Il arrive aussi
que l'on ait à considérer la totalité des éléments qui appartienent
à un ensemble E ou à un ensemble F. Dans ce cas, on définira
l'ensemble G qui contient tous ces éléments comme la réunion
de E et de F : on écrira G = E 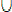 F, et on lira "G égale E union F".
F, et on lira "G égale E union F".
-
Réunion
G des ensembles E et F.
G
= {a, b, c, d, e}.
 Les
ensembles E et F sont tous les deux inclus dans G (ce sont deux sous-ensembles
de G) : E Les
ensembles E et F sont tous les deux inclus dans G (ce sont deux sous-ensembles
de G) : E  G et F
G et F  G.
G.
 Deux
ensembles E et F sont égaux (E = F) si et seulement si on a à
la fois E Deux
ensembles E et F sont égaux (E = F) si et seulement si on a à
la fois E  F et F
F et F  E. Dans le cas contraire ils sont distincts (E
E. Dans le cas contraire ils sont distincts (E 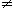 F).
F).
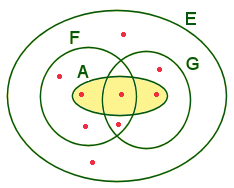
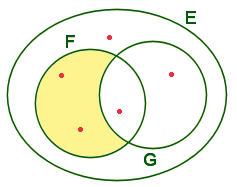
Recouvrement
et partition.
Lorsque la réunion F de sous-ensembles
non vides d'un ensemble E contient un sous-ensemble A, on dit que F est
un recouvrement de A.
Lorsque plusieurs sous-ensembles non vides
d'un ensemble E sont tous disjoints deux à deux et que leur réunion est
égale à E, on dit qu'ils forment une partition de E.
 |
 |
|
Recouvrement.
- F et G recouvrent l'ensemble A car tous les éléments de A appartiennent
à la réunion de F et G.
|
Partition.
- F et G forment une partition de E, car leur intersection est vide et
leur réunion est égale à E.
|
 Une
partition est donc un cas particulier de recouvrement, dans lequel les
sous-ensembles consid√©r√©s sont disjoints et o√Ļ l'ensemble recouvert
est E lui-même. Une
partition est donc un cas particulier de recouvrement, dans lequel les
sous-ensembles consid√©r√©s sont disjoints et o√Ļ l'ensemble recouvert
est E lui-même.
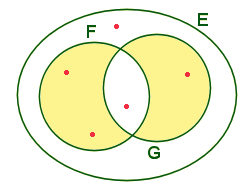
Différence. Complémentarité.
Différence
et différence symétrique de deux ensembles.
On défini la différence
de deux ensembles F et G quelconques, notée F \ G comme l'ensemble des
√©l√©ments de F auxquels on a √īt√© les √©l√©ments de F  G.
G.
La différence symétrique
de deux ensembles F et G, notée F  G est, quant à elle, l'ensemble des éléments de F U G qui n'appartiennent
pas à leur intersection F
G est, quant à elle, l'ensemble des éléments de F U G qui n'appartiennent
pas à leur intersection F  G. On a donc F
G. On a donc F  G = (F U G) \ (F
G = (F U G) \ (F  G).
G).
-
 |
 |
|
Différence
de deux ensembles. - C'est l'ensemble des éléments de F qui n'appartiennent
pas aussi à G
|
Différence
symétrique de deux ensembles. - C'est l'ensemble des éléments qui
appartiennent à la réunion de F et G mais pas à leur intersection.
|
Ensembles
complémentaires.
Dans le cas o√Ļ
F est une sous ensemble de E (soit F  E), les éléments de E qui n'appartiennent pas à F appartiennent
à l'ensemble particulier appelé l'ensemble complémentaire de
F par rapport à E. Parmi les façons de noter un ensemble complémentaire,
on retiendra celle-ci : G =
E), les éléments de E qui n'appartiennent pas à F appartiennent
à l'ensemble particulier appelé l'ensemble complémentaire de
F par rapport à E. Parmi les façons de noter un ensemble complémentaire,
on retiendra celle-ci : G =  EF
(qui se lit : "G est le complémentaire de F par rapport à E"). EF
(qui se lit : "G est le complémentaire de F par rapport à E").
-
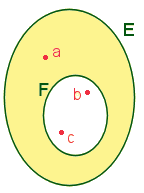
Complémentaire
de l'ensemble F
dans
l'ensemble E : G = {a}.
 Dire
que G est le complémentaire de F dans E est équivalent à dire que F
est le complémentaire de G dans E : Dire
que G est le complémentaire de F dans E est équivalent à dire que F
est le complémentaire de G dans E :
G = 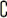 EF EF  F =
F = 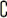 EG. EG.
 Le complémentaire
de l'ensemble vide par rapport à E est égal à E, et de même le complémentaire
de E par rapport à E est égal à l'ensemble vide : Le complémentaire
de l'ensemble vide par rapport à E est égal à E, et de même le complémentaire
de E par rapport à E est égal à l'ensemble vide :
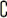 E E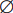 = E et
= E et 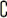 EE
= EE
= 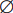 . .
 Dans
certains contextes, l'écriture peut être allégée en convenant d'utiliser
le signe moins "-" : ainsi G = Dans
certains contextes, l'écriture peut être allégée en convenant d'utiliser
le signe moins "-" : ainsi G = 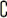 EF
pourra se noter simplement G = E - F. EF
pourra se noter simplement G = E - F.
Lois
de De Morgan pour les ensembles.
Dans le cas de deux
ensembles quelconques A et B, avec G = A\B, les égalités suivante, appelées
lois
de De Morgan, sont vérifiées :
G\ (A U
B) = (G\A)  (G\B) (G\B)
G\ (A  B) = (G\A) U (G\B)
B) = (G\A) U (G\B)
Si A et B sont deux
sous ensembles d'un ensemble E, les lois de De Morgan peuvent s'écrire
:
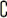 E(A
U B) = E(A
U B) = 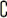 E(A) E(A)  '
'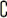 E
(B). E
(B).
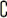 E(A E(A  B) =
B) = 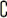 E(A)
U E(A)
U 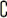 E
(B). E
(B).
Ensembles de nombres.
Les nombres et les
ensembles de nombres jouent un r√īle central dans les math√©matique, dont
de larges pans sont consacrés à leur étude. Aussi certains de ces ensembles
sont-ils désignés des symboles particuliers, d'usage très courant.
Ensembles
des nombres entiers naturels.
Les nombres dont on se sert pour compter
les objets sont appelés nombres entiers naturels (ou simplement
entiers
naturels). L'ensemble dans lequel on les range, ainsi que le zéro
(0) est appelé  :
:
 = {0, 1, 2, 3, 4, ...}
= {0, 1, 2, 3, 4, ...}
On note 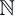 *
("N étoile"), l'ensemble des entiers strictement positifs,
c'est-√†-dire l'ensemble des entiers naturels auquel on a √īt√© le z√©ro
: *
("N étoile"), l'ensemble des entiers strictement positifs,
c'est-√†-dire l'ensemble des entiers naturels auquel on a √īt√© le z√©ro
:
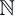 *
= *
=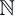 - {0}
- {0}
Lorsqu'on additionne deux entiers naturels,
le résultat est toujours un entier naturel. Cela n'est plus vrai lorsqu'on
soustrait deux nombres de 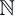 .
Certaines soustractions ne conduisent pas à un résultat dans .
Certaines soustractions ne conduisent pas à un résultat dans 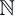 (par exemple 4 - 3 = ?). Pour que ces opérations aient un sens,
il faut considérer un autre ensemble, dans lequel
(par exemple 4 - 3 = ?). Pour que ces opérations aient un sens,
il faut considérer un autre ensemble, dans lequel 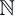 est inclus : l'ensemble des nombres entiers relatifs.
est inclus : l'ensemble des nombres entiers relatifs.
Ensemble
des nombre entiers ou nombres entiers relatifs.
L'ensemble des nombres entiers relatifs,
représenté par le symbole 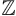 ,
comprend tous les entiers naturels ( ,
comprend tous les entiers naturels (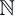 ' ' 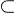 ' '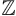 ),
et tous les nombres définis comme le résultat de la soustraction 0 -
n, o√Ļ 0 est le nombre z√©ro et o√Ļ n est un entier naturel strictement
positif (appartenant donc à ),
et tous les nombres définis comme le résultat de la soustraction 0 -
n, o√Ļ 0 est le nombre z√©ro et o√Ļ n est un entier naturel strictement
positif (appartenant donc à 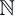 *).
Les nombres ainsi définis forment l'ensemble des nombres entiers strictement
négatifs; il se note par *).
Les nombres ainsi définis forment l'ensemble des nombres entiers strictement
négatifs; il se note par 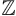 -.
On a ainsi : -.
On a ainsi :
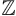 =
= 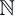 U
U 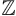 - -
Ensemble
des nombres rationnels.
De la même façon que l'on ne pouvait
pas donner le résultat dans 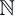 de toute soustraction de nombres appartenant à
de toute soustraction de nombres appartenant à 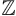 ,
on ne peut donner le produire dans ,
on ne peut donner le produire dans 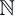 celui de la division de deux nombres appartenant à
celui de la division de deux nombres appartenant à 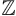 (l'entier par lequel on divise ne pouvant être 0); trois divisé par deux,
par exemple, n'est pas un nombre entier. L'ensemble de nombres qui contient
non seulement tous les entiers, mais aussi les nombres de telles divisions
est l'ensemble des nombres rationnels; il est noté
(l'entier par lequel on divise ne pouvant être 0); trois divisé par deux,
par exemple, n'est pas un nombre entier. L'ensemble de nombres qui contient
non seulement tous les entiers, mais aussi les nombres de telles divisions
est l'ensemble des nombres rationnels; il est noté 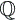 et ses éléments sont tous les nombres qui sont le résultat de la division
de deux entiers quelconques.
et ses éléments sont tous les nombres qui sont le résultat de la division
de deux entiers quelconques.
Ensemble
des nombres réels.
Tous les nombres ne peuvent cependant
pas s'écrire comme le résultat d'une division entre deux entiers. C'est
les cas , par exemple, de 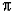 = 3,1415926... ou de
= 3,1415926... ou de 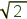 = 1,4142135... Cela conduit à admettre une autre ensemble, qui contient
tous les éléments de
= 1,4142135... Cela conduit à admettre une autre ensemble, qui contient
tous les éléments de  ,
mais aussi des nombres tels que ,
mais aussi des nombres tels que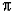 ou
ou 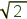 .
Ce sera l'ensemble que l'on appellera l'ensemble des nombres réels.
Cet ensemble, noté .
Ce sera l'ensemble que l'on appellera l'ensemble des nombres réels.
Cet ensemble, noté 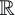 ,
est plus difficile à définir que les ensembles de nombres mentionnés
jusqu'ici. Les différences entre ,
est plus difficile à définir que les ensembles de nombres mentionnés
jusqu'ici. Les différences entre 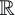 et
et 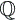 font appel à la distinction de notions assez abstraites de densité
et de complétude. Un ensemble de nombres est dit dense lorsqu'entre
deux nombres, aussi proches l'un de l'autre que l'on voudra, on peut encore
trouver un nombre (et même une infinité de nombres), et c'est bien le
cas de
font appel à la distinction de notions assez abstraites de densité
et de complétude. Un ensemble de nombres est dit dense lorsqu'entre
deux nombres, aussi proches l'un de l'autre que l'on voudra, on peut encore
trouver un nombre (et même une infinité de nombres), et c'est bien le
cas de 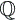 ,
contrairement à ,
contrairement à 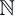 '
et' '
et'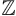 (aucun nombre entier ne peut être inséré entre 1 et 2, par exemple).
Quant à
(aucun nombre entier ne peut être inséré entre 1 et 2, par exemple).
Quant à 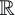 ,
lorsqu'on considère deux de ses nombres aussi proches que l'on veut, on
en arrive à pouvoir envisager (pour employer une image plus intuitive
que mathématique) qu'ils se touchent : il n'y a pas de place alors pour
insérer entre eux de nouveaux nombres. On dit alors que ,
lorsqu'on considère deux de ses nombres aussi proches que l'on veut, on
en arrive à pouvoir envisager (pour employer une image plus intuitive
que mathématique) qu'ils se touchent : il n'y a pas de place alors pour
insérer entre eux de nouveaux nombres. On dit alors que 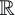 est complet.
est complet.
Ensemble
des nombres complexes.
L'ensemble 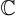 des
nombres
complexes se définit à partir de des
nombres
complexes se définit à partir de 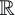 ,
en revenant à l'idée qu'une opération appliquée à certains nombres
peut n'aboutir à aucun résultat. Ainsi la racine carrée y
de x (notée ,
en revenant à l'idée qu'une opération appliquée à certains nombres
peut n'aboutir à aucun résultat. Ainsi la racine carrée y
de x (notée 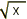 )
est le nombre y tel que y.y = y² = x. Les règles de la multiplication
(.) dans )
est le nombre y tel que y.y = y² = x. Les règles de la multiplication
(.) dans 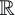 font que x est toujours positif. Un nombre négatif n'a donc pas de racine
carrée dans
font que x est toujours positif. Un nombre négatif n'a donc pas de racine
carrée dans 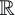 .
Il est cependant possible d'introduire un nouveau nombre que l'on notera
i
et tel que i.i = i² = -1 et qui n'appartient pas à .
Il est cependant possible d'introduire un nouveau nombre que l'on notera
i
et tel que i.i = i² = -1 et qui n'appartient pas à 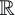 : i est l'unité des nombres dits imaginaires,
tous ces nombres s'obtenant en multipliant i par un nombre réel.
L'ensemble
: i est l'unité des nombres dits imaginaires,
tous ces nombres s'obtenant en multipliant i par un nombre réel.
L'ensemble 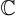 peut alors être défini comme l'ensemble de tous les nombres
z
de type z = a + i.b, o√Ļ a et b sont des nombres r√©els. Si a = 0,
z
= ib est un nombre imaginaire pur, mais si b = 0, z = a est un nombre
réel. Ainsi l'ensemble
peut alors être défini comme l'ensemble de tous les nombres
z
de type z = a + i.b, o√Ļ a et b sont des nombres r√©els. Si a = 0,
z
= ib est un nombre imaginaire pur, mais si b = 0, z = a est un nombre
r√©el. Ainsi l'ensemble  appara√ģt-il comme un ensemble inclus dans
appara√ģt-il comme un ensemble inclus dans  . .
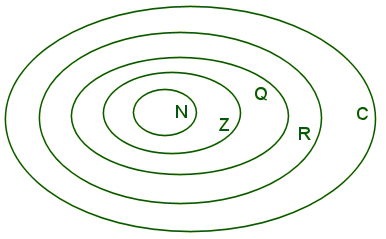
Principaux
ensembles de nombres.
Relations
La théorie des ensemble
ne serait rien que si elle ne reposait que sur des ensembles et des élements.
Sa fécondité vient des nombreuses mises en correspondance que l'on peut
établir entre éléments, entre éléments et ensembles et entre ensembles.
Plusieurs de ces correspondances (égalité, appartenance, inclusion, réunion,
complémentarité) viennent d'être évoquées. Elles répondent à la
notion très générale de relation.
Définitions.
Relations.
Une relation
binaire est une correspondance que l'on établit entre les éléments
de deux ensembles, un ensemble de départ ou source, et un ensemble d'arrivée,
ensemble image ou but, quand une propriété donnée est vérifiée entre
ces éléments. Il est entendu que rien ne s'oppose à ce ce que l'ensemble
de départ soit identique à l'ensemble d'arrivée, autrement dit à ce
que la relation puisse être définie entre éléments appartenant au même
ensemble.
Soit ainsi x
un élément appartenant à l'ensemble E de départ et y une élément
appartenant à l'ensemble F d'arrivée, et soit la relation  définie lorsque la propriété considérée est vérifiée, on écrira
: x
définie lorsque la propriété considérée est vérifiée, on écrira
: x  y pour
signifier que x est en relation avec y. y pour
signifier que x est en relation avec y.
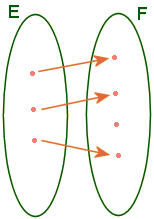
Diagramme
sagittal d'une relation.
Une relation est
représentée graphiquement par une flèche (en latin
sagitta =
flèche) tracée entre les deux éléments x et y mis en correspondance
par la relation : une flèche va de x à y si et seulement si x  y.
y.
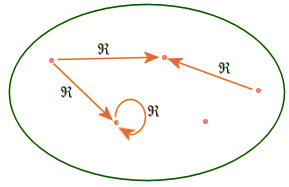
Diagramme
sagittal d'une relation.
Produit
cartésien.
Si l'on considère
un ensemble E et un ensemble F, et la relation  qui met en correspondance des élément de E avec les éléments de F (pas
nécessairement tous les éléments), on est conduit à s'intéresser à
tous les couples (x, y) d'éléments tels que x appartienne à E et
y à F. L'ensemble de ces couples est appelé le produit cartésien
des deux ensembles considérés, et sera noté E X
F. Dans le cas o√Ļ la relation est d√©finie entre √©l√©ments d'un m√™me
ensemble E, la notion de produit cartésien existe encore. On l'écrit
: E X E, ou, par analogie avec l'élévation
au carré des nombres, E².
qui met en correspondance des élément de E avec les éléments de F (pas
nécessairement tous les éléments), on est conduit à s'intéresser à
tous les couples (x, y) d'éléments tels que x appartienne à E et
y à F. L'ensemble de ces couples est appelé le produit cartésien
des deux ensembles considérés, et sera noté E X
F. Dans le cas o√Ļ la relation est d√©finie entre √©l√©ments d'un m√™me
ensemble E, la notion de produit cartésien existe encore. On l'écrit
: E X E, ou, par analogie avec l'élévation
au carré des nombres, E².
 L'ordre
dans lequel on écrit les deux termes du couple a son importance, car,
sauf cas particulier d'une relation dite symétrique (V. ci-dessous);
on a-: x L'ordre
dans lequel on écrit les deux termes du couple a son importance, car,
sauf cas particulier d'une relation dite symétrique (V. ci-dessous);
on a-: x  y
y 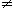 y y  x. Cela explique que lorsqu'on considère le couple (x, y) on le qualifie
de paire ordonnée. Dans le couple (x, y), x est la première
coordonnée et y la deuxième coordonnée. Si (x, y)'
x. Cela explique que lorsqu'on considère le couple (x, y) on le qualifie
de paire ordonnée. Dans le couple (x, y), x est la première
coordonnée et y la deuxième coordonnée. Si (x, y)'  ' ' 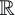 X X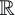 =
= 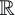 ², la première
coordonnée est souvent appelée l'abscisse, et la deuxième, l'ordonnée. ², la première
coordonnée est souvent appelée l'abscisse, et la deuxième, l'ordonnée.
 Le
produit cartésien a été entendu jusqu'ici entre deux ensembles seulement
(ou entre un ensemble et lui-même). Mais cette notion peut être étendue
à n ensembles (E1, E2,
E3, ..., En). On note alors leur
produit cartésien : E1 X
E2 X
E3 X
...X En;
les éléments de celui-ci sont appelés n-uplets. (couples
ou doublets quand n = 2, triplets quand n=3). Le
produit cartésien a été entendu jusqu'ici entre deux ensembles seulement
(ou entre un ensemble et lui-même). Mais cette notion peut être étendue
à n ensembles (E1, E2,
E3, ..., En). On note alors leur
produit cartésien : E1 X
E2 X
E3 X
...X En;
les éléments de celui-ci sont appelés n-uplets. (couples
ou doublets quand n = 2, triplets quand n=3).
 On
a définio jusqu'ici une relation comment une correspondance entre des
éléments d'ensembles. Mais une relation définie entre ensembles. Le
produit cartésien (X) de deux ensembles en est un
exemple; même constat pour la relation d'inclusion (notée On
a définio jusqu'ici une relation comment une correspondance entre des
éléments d'ensembles. Mais une relation définie entre ensembles. Le
produit cartésien (X) de deux ensembles en est un
exemple; même constat pour la relation d'inclusion (notée 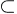 ).
Quant à l'appartenance (notée ).
Quant à l'appartenance (notée  ),
elle peut se comprendre comme un exemple de relation entre un élément
et un ensemble. ),
elle peut se comprendre comme un exemple de relation entre un élément
et un ensemble.
 Dans
le cas de deux ensembles E et F possédant chacun un nombre fini d'éléments,
si l'ensemble E possède n éléments et si l'ensemble F en possède
m,
alors E X F possède
n.m éléments (" . " est le symbole de la multiplication de
nombres). Dans
le cas de deux ensembles E et F possédant chacun un nombre fini d'éléments,
si l'ensemble E possède n éléments et si l'ensemble F en possède
m,
alors E X F possède
n.m éléments (" . " est le symbole de la multiplication de
nombres).
Graphe
d'une relation.
Tous les éléments de E X
F, autrement dit tous les couples (x, y) ne sont pas nécessairement
mis en correspondance la relation  .
Les couples qui sont ainsi reliés appartiennent à un sous-ensemble de
E X F appelé le graphe de la relation.
On
pourra dire qu'une paire (x, y) appartenant au produit cartésien E X
F a ses termes mis en correspondance par relation .
Les couples qui sont ainsi reliés appartiennent à un sous-ensemble de
E X F appelé le graphe de la relation.
On
pourra dire qu'une paire (x, y) appartenant au produit cartésien E X
F a ses termes mis en correspondance par relation  si et seulement si (x, y) appartient au graphe G de cette relation.
si et seulement si (x, y) appartient au graphe G de cette relation.
 Ainsi,
une relation binaire Ainsi,
une relation binaire  est enti√®rement connue si l'on conna√ģt E x F et G, ce que l'on exprime
cela en écrivant
est enti√®rement connue si l'on conna√ģt E x F et G, ce que l'on exprime
cela en écrivant  = (E, F, G). Le triplet (E, F, G) prend le nom de correspondance
entre E et F.
= (E, F, G). Le triplet (E, F, G) prend le nom de correspondance
entre E et F.
 Réciproquement,
lorsque l'on considère n'importe quel sous-ensemble G du produit cartésien
E X F, on définit en
même temps une relation binaire. Réciproquement,
lorsque l'on considère n'importe quel sous-ensemble G du produit cartésien
E X F, on définit en
même temps une relation binaire.
 Deux
correspondances ou deux relations Deux
correspondances ou deux relations  = (E, F, G) et
= (E, F, G) et  '
= (E', F', G') sont égales si et seulement si E = E' et F = F' et G =
G'. '
= (E', F', G') sont égales si et seulement si E = E' et F = F' et G =
G'.
Relation
réciproque.
Dans la relation  = (E, F, G), les éléments de G sont des éléments de E mis en correspondance
avec des éléments de F. Mais on peut aussi s'intéresser à la correspondance
que cela induit entre les éléments de F et des éléments de E. Le graphe,
noté G-1, de cette nouvelle relation,
notée
= (E, F, G), les éléments de G sont des éléments de E mis en correspondance
avec des éléments de F. Mais on peut aussi s'intéresser à la correspondance
que cela induit entre les éléments de F et des éléments de E. Le graphe,
noté G-1, de cette nouvelle relation,
notée  -1,
sera ainsi le sous-ensemble des couples de F X E tels
que ces couples appartiennent à G. -1,
sera ainsi le sous-ensemble des couples de F X E tels
que ces couples appartiennent à G.  -1
=
(F, E, G-1) sera appelée la relation
réciproque de -1
=
(F, E, G-1) sera appelée la relation
réciproque de  . .
Relation
composée.
Soient deux relations  = (E, F, G) et
= (E, F, G) et  '
= (F, H, G') telles que l'ensemble d'arrivée F de la première soit l'ensemble
de départ de la seconde, on peut définir une relation '
= (F, H, G') telles que l'ensemble d'arrivée F de la première soit l'ensemble
de départ de la seconde, on peut définir une relation  "
dont l'ensemble de départ est E est l'ensemble de départ de la première
relation et l'ensemble d'arrivée est l'esemble d'arrivée de la seconde,
c'est-à-dire H. On aura ainsi "
dont l'ensemble de départ est E est l'ensemble de départ de la première
relation et l'ensemble d'arrivée est l'esemble d'arrivée de la seconde,
c'est-à-dire H. On aura ainsi  "
= (E, H, G"), o√Ļ G" est l'ensemble des √©l√©ments (x, y) de E X
H, tels qu'il existe un élément y appartenant à F, avec (x, y) appartenant
à G et (y, z) appartenant à G'. On appelle "
= (E, H, G"), o√Ļ G" est l'ensemble des √©l√©ments (x, y) de E X
H, tels qu'il existe un élément y appartenant à F, avec (x, y) appartenant
à G et (y, z) appartenant à G'. On appelle "
la relation composée des relations "
la relation composée des relations  et
et  '. '.
Propriétés des
relations.
Les relations peuvent
posséder certaines des propriétés suivantes :
Réflexivité.
Une relation  est réflexive lorsque
est réflexive lorsque  x x  E : x
E : x  x
(x est en relation avec x). Par exemple, dans une fratrie,
la relation "est de la famille de" est réflexive, mais la relation
"est le frère ou la soeur de" ne l'est pas. x
(x est en relation avec x). Par exemple, dans une fratrie,
la relation "est de la famille de" est réflexive, mais la relation
"est le frère ou la soeur de" ne l'est pas.
 La
réflexivité peut aussi être définie pour la relation d'inclusion (au
sens large) entre deux ensembles E quelconques : E La
réflexivité peut aussi être définie pour la relation d'inclusion (au
sens large) entre deux ensembles E quelconques : E 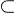 E.
E.
Symétrie
et antisymétrie.
Une relation  est symétrique lorsque
est symétrique lorsque  (x, y)
(x, y)  E X
F : x E X
F : x  y y 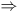 y
y  x (si
x
est en relation avec y alors y est en relation avec
x).
Par exemple la relation "est le frère ou la soeur de" est symétrique,
mais les relations " est le frère de" ou "est la soeur de" ne sont pas
symétriques dans l'ensemble considéré. x (si
x
est en relation avec y alors y est en relation avec
x).
Par exemple la relation "est le frère ou la soeur de" est symétrique,
mais les relations " est le frère de" ou "est la soeur de" ne sont pas
symétriques dans l'ensemble considéré.
Une relation  est antisymétrique lorsque
est antisymétrique lorsque  (x, y)
(x, y)  E : (x E : (x  y et y
y et y  x) x) 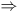 x = y (si x est en relation avec y et y est en relation
avec x alors x égale y).
x = y (si x est en relation avec y et y est en relation
avec x alors x égale y).
 La
relation d'inclusion qui met en correspondance deux ensembles est une relation
antisymétrique : si E est inclus dans F et F est inclus dans E, alors
E égale F. La
relation d'inclusion qui met en correspondance deux ensembles est une relation
antisymétrique : si E est inclus dans F et F est inclus dans E, alors
E égale F.
Notez bien que ne pas
être symétrique n'est pas synonyme d'être antisymétrique.
Transitivité.
Une relation  est transitive lorsque
est transitive lorsque  x,
y, z : (x x,
y, z : (x  y et y
y et y  z) z) 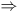 x
x  z. La
relation "est la soeur de" est transitive dans l'ensemble {Sophie, Maud,
Géraldine} : Odélia est la soeur de Maud et Maud est la soeur de Géraldine,
implique qu'Odélia est la soeur de Géraldine. z. La
relation "est la soeur de" est transitive dans l'ensemble {Sophie, Maud,
Géraldine} : Odélia est la soeur de Maud et Maud est la soeur de Géraldine,
implique qu'Odélia est la soeur de Géraldine.
 La
relation d'inclusion définie entre ensembles est une relation transitive
: si E est inclus dans F et F est inclus dans G, alors E est inclus dans
G.
- La
relation d'inclusion définie entre ensembles est une relation transitive
: si E est inclus dans F et F est inclus dans G, alors E est inclus dans
G.
-
| Réflexivité. |
Symétrie. |
Transitivité.
|
Relations d'équivalence.
Une relation binaire  définie sur un ensemble E est une relation d'équivalence si et
seulement si
définie sur un ensemble E est une relation d'équivalence si et
seulement si  est : réflexive, symétrique et transitive.
est : réflexive, symétrique et transitive.
 L'identité
= de deux ensembles E et F (ou de deux éléments) est une relation d'équivalence
: elle est réflexive (E = E); elle est symétrique (E = F L'identité
= de deux ensembles E et F (ou de deux éléments) est une relation d'équivalence
: elle est réflexive (E = E); elle est symétrique (E = F  F = E; elle est transitive : (E = F et F = G)
F = E; elle est transitive : (E = F et F = G)  E = G.
E = G.
 Pour
noter une relation d'équivalence on utilise souvent le symbole ~ (par
exemple : x ~ y). Une autre façon d'exprimer que deux éléments sont
reliés par une relation d'équivalence est la suivante : x Pour
noter une relation d'équivalence on utilise souvent le symbole ~ (par
exemple : x ~ y). Une autre façon d'exprimer que deux éléments sont
reliés par une relation d'équivalence est la suivante : x  y (mod
y (mod  ),
qui se lit "x et y sont équivalents (ou congrus)
modulo' ),
qui se lit "x et y sont équivalents (ou congrus)
modulo'  ". ".
Classes
d'équivalence. Partition. Ensemble quotient.
Un relation d'équivalence
divise l'ensemble dans lequel elle est définie en un certain nombre de
sous-ensembles disjoints deux à deux (c'est-à-dire qui n'ont aucun élément
en commun) que l'on appelle des classes d'équivalence (ou si l'on
veut être plus précis : classes d'équivalence modulo  ). ).
 Tous
les éléments d'une classe d'équivalence étant reliés entre eux, il
suffit de mentionner un élément quelconque de cette classe, disons a,
appelé représentant de la classe, pour que la classe entière
puisse être définie. On pourra alors la noter, par exemple, [a], å ou
encore Cl Tous
les éléments d'une classe d'équivalence étant reliés entre eux, il
suffit de mentionner un élément quelconque de cette classe, disons a,
appelé représentant de la classe, pour que la classe entière
puisse être définie. On pourra alors la noter, par exemple, [a], å ou
encore Cl (a).
(a).
Lorsque l'on réunit
toutes ces classes d'équivalence d'un ensemble E on obtient l'ensemble
E lui-même, ce que l'on exprime en disant que la relation vérifie une
partition
de l'ensemble E.
Les parties de E définies par la relation  sont les éléments d'un ensemble appelé ensemble quotient et noté
E/
sont les éléments d'un ensemble appelé ensemble quotient et noté
E/ . .
Relations d'ordre.
Les relations d'ordre
sont, avec les relations d'équivalence, un autre grand type de relations
étudiées en mathématiques.
Une relation binaire  est une relation d'ordre si et seulement si
est une relation d'ordre si et seulement si  est : réflexive, antisymétrique et transitive.
est : réflexive, antisymétrique et transitive.
 Pour
noter les relations d'ordre, on renonce au symbole Pour
noter les relations d'ordre, on renonce au symbole  pour le remplacer par le symbole
pour le remplacer par le symbole 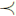 qui rappelle le symbole
qui rappelle le symbole 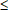 utilisé pour ordonner les éléments de l'ensemble des nombres réels
utilisé pour ordonner les éléments de l'ensemble des nombres réels 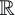 et de ses sous-ensembles.
et de ses sous-ensembles.  et
et 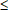 se lisent
de la même façon. Ainsi x se lisent
de la même façon. Ainsi x 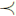 y se lira-t-il "x inférieur à y" ou "y supérieur à x" (on trouve aussi
parfois les lectures, peut-être préférables : "x antérieur à x" et
"y postérieur à x").
y se lira-t-il "x inférieur à y" ou "y supérieur à x" (on trouve aussi
parfois les lectures, peut-être préférables : "x antérieur à x" et
"y postérieur à x").
 Le
sens particulier de certaines relations d'ordre peut aussi induire des
notations différentes. Par exemple, dans Le
sens particulier de certaines relations d'ordre peut aussi induire des
notations différentes. Par exemple, dans 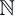 *,
la relation "x divise y" est une relation d'ordre et se note x|y; même
chose pour l'inclusion au sens large dans l'ensemble des parties d'un ensemble,
qui est aussi une relation d'ordre et se note, comme on l'a vu A *,
la relation "x divise y" est une relation d'ordre et se note x|y; même
chose pour l'inclusion au sens large dans l'ensemble des parties d'un ensemble,
qui est aussi une relation d'ordre et se note, comme on l'a vu A 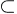 B.
B.
L'ordre peut être partiel
ou total.
Ordre
total.
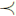 munit l'ensemble E d'un ordre total si pour tout couple d'éléments (x
,y) de ensemble E X E, on a x
munit l'ensemble E d'un ordre total si pour tout couple d'éléments (x
,y) de ensemble E X E, on a x 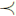 y ou y
y ou y 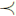 x. Tous les éléments peuvent donc être mis en relation les uns avec
les autres : il peuvent être comparés et l'ensemble E est dit
totalement
ordonné.
x. Tous les éléments peuvent donc être mis en relation les uns avec
les autres : il peuvent être comparés et l'ensemble E est dit
totalement
ordonné.
 On l'a vu plus haut, quand on travaille sur des nombres réels, on utilise
fréquement la relation
On l'a vu plus haut, quand on travaille sur des nombres réels, on utilise
fréquement la relation 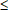 ,
qui se lit "est inférieur à" ou "est inférieur ou égal à". Il
s'agit d'une relation d'ordre total : elle permet d'ordonner tous les nombres
les uns par rapport aux autres (x et y étant deux nombres réels, on peut
toujours dire que : soit x ,
qui se lit "est inférieur à" ou "est inférieur ou égal à". Il
s'agit d'une relation d'ordre total : elle permet d'ordonner tous les nombres
les uns par rapport aux autres (x et y étant deux nombres réels, on peut
toujours dire que : soit x 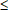 y, soit y
y, soit y 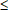 x). Tous les réels sont dits comparables.
x). Tous les réels sont dits comparables.
 Une
autre relation qui ressemble à celle-ci peut s'énoncer : "est strictement
inférieur à", et elle se note <. Elle aussi permet de comparer les
nombres et on la qualifie de relation d'ordre strict, mais il est
à remarquer qu'en réalité
ce n'est pas une relation d'ordre (elle
n'est pas réflexive). Une
autre relation qui ressemble à celle-ci peut s'énoncer : "est strictement
inférieur à", et elle se note <. Elle aussi permet de comparer les
nombres et on la qualifie de relation d'ordre strict, mais il est
à remarquer qu'en réalité
ce n'est pas une relation d'ordre (elle
n'est pas réflexive).
 On
peut encore associer à la relation On
peut encore associer à la relation 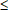 sa relation opposée
sa relation opposée 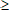 (qui se lit "est supérieur ou égal à") : on a x
(qui se lit "est supérieur ou égal à") : on a x 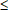 y
y 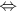 y
y 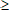 x. Malgré
cette équivalence, l'utilisation de x. Malgré
cette équivalence, l'utilisation de 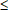 ou de
ou de 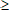 (ou
de < ou de >) n'est pas indifférente. Par exemple, lorsqu'on cherche
"le plus petit élément" de l'ensemble des entiers naturels (c'est-à-dire
x | (ou
de < ou de >) n'est pas indifférente. Par exemple, lorsqu'on cherche
"le plus petit élément" de l'ensemble des entiers naturels (c'est-à-dire
x |  y : x y : x 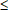 y) celui-ci existe, c'est 0, et l'on dit que l'ensemble des entiers naturel
est bien ordonné (par la relation
y) celui-ci existe, c'est 0, et l'on dit que l'ensemble des entiers naturel
est bien ordonné (par la relation 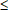 ). Mais on se trouve dans une impasse dès que l'on cherche "le plus grand
élément" de cet ensemble (c'est-à-dire x |
). Mais on se trouve dans une impasse dès que l'on cherche "le plus grand
élément" de cet ensemble (c'est-à-dire x |  y
: x y
: x 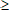 y). y).
Ordre
partiel.
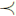 munit l'ensemble E d'un ordre partiel (ou
munit l'ensemble E d'un ordre partiel (ou 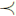 est un ordre partiel sur E) lorsqu'il existe des couples (x, y)
de l'ensemble produit E² tels que ni x
est un ordre partiel sur E) lorsqu'il existe des couples (x, y)
de l'ensemble produit E² tels que ni x 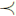 y, ni y
y, ni y 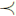 x.
x.
 La
relation d'inclusion sur l'ensembles des parties d'un ensemble est un exemple
d'ordre partiel. La
relation d'inclusion sur l'ensembles des parties d'un ensemble est un exemple
d'ordre partiel.
Eléments
remarquables d'un ensemble ordonné.
Soient F un sous-ensemble non vide de
E et 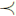 une relation d'ordre partiel sur E. On appelle majorant de F tout
élément s de E tel que quelque soit x appartenant à F,
on ait x
une relation d'ordre partiel sur E. On appelle majorant de F tout
élément s de E tel que quelque soit x appartenant à F,
on ait x 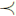 s. de même, on appelle minorant de F tout élément
s de
E tel que quelque soit x appartenant à F, on ait s
s. de même, on appelle minorant de F tout élément
s de
E tel que quelque soit x appartenant à F, on ait s 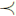 x.
x.
S'il existe dans un ensemble ordonné E
un élément g supérieur à tous les autres ( x
x  E
: x E
: x 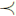 g), g est appelé le plus grand élément de E. S'il existe dans
E un élément p inférieur à tous les autres (
g), g est appelé le plus grand élément de E. S'il existe dans
E un élément p inférieur à tous les autres ( x
x  E
: p E
: p 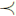 x), p est appelé le plus petit élément de E. Dans tous les cas,
p et g sont uniques. L'élément m d'un ensemble E sera dit maximal
si pour tout x appartenant à E, x
x), p est appelé le plus petit élément de E. Dans tous les cas,
p et g sont uniques. L'élément m d'un ensemble E sera dit maximal
si pour tout x appartenant à E, x 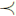 m implique x = m; il sera dit minimal si si pour tout
x
appartenant à E, m
m implique x = m; il sera dit minimal si si pour tout
x
appartenant à E, m 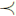 x implique x = m.
x implique x = m.
 Soit
E un ensemble non vide muni d'une relation d'ordre partiel Soit
E un ensemble non vide muni d'une relation d'ordre partiel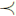 .
Si tout sous-ensemble de E totalement ordonné par .
Si tout sous-ensemble de E totalement ordonné par 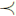 admet un majorant, alors E possède un élément maximal. (Ce théorème
est connu sous le nom de Lemme de Zorn).
admet un majorant, alors E possède un élément maximal. (Ce théorème
est connu sous le nom de Lemme de Zorn).
Lorsqu'il existe, le
plus petit des majorants d'une partie majorée F de de E est appelé la
borne supérieure de F; le plus grand des minorants, lorsqu'il existe,
est la borne inférieure de F. Ces bornes sont notées respectivement supE
F ("sup de F dans E") et infE F ("inf de F dans
E").
 Un
ensemble ordonné E qui possède à la fois une borne supérieure supE
et une borne inférieure infE est appelé un treillis
(synonymes : ensemble réticulé, lattis ou lattice
en anglais). Un
ensemble ordonné E qui possède à la fois une borne supérieure supE
et une borne inférieure infE est appelé un treillis
(synonymes : ensemble réticulé, lattis ou lattice
en anglais).
Applications
(fonctions)
Nomenclature, notations.
Nomenclature.
Une relation  d'un ensemble E, source, vers un ensemble F, image, est dite relation
fonctionnelle si chaque élément x de E est associé par cette
relation à un élément y au plus dans F.
d'un ensemble E, source, vers un ensemble F, image, est dite relation
fonctionnelle si chaque élément x de E est associé par cette
relation à un élément y au plus dans F.
Lorsque tous
les éléments de E sont mis en correspondance avec un élément de F,
cette sorte de relation est appelée application ou
fonction.
Application est un terme général, l'usage tendant à réserver le nom
de fonction aux seules applications définies
sur des ensembles de nombres.
Ecriture.
On utilise ordinairement
une écriture particulière pour désigner les applications (et les fonctions).
La notation habituelle  est abandonnée et l'on utilise souvent la lettre f, quand une seule
application est impliquée (la lettre g est aussi utilisée quand
il y en a deux, etc.). Ainsi, (étant toujours entendu que (x, y)
est abandonnée et l'on utilise souvent la lettre f, quand une seule
application est impliquée (la lettre g est aussi utilisée quand
il y en a deux, etc.). Ainsi, (étant toujours entendu que (x, y)  E X F), ce que nous avons écrit jusqu'ici x
E X F), ce que nous avons écrit jusqu'ici x  y s'écrira désormais
y s'écrira désormais  (x) = y ou, de manière encore plus courante, en utilisant la lettre
f
:
(x) = y ou, de manière encore plus courante, en utilisant la lettre
f
:
f
(x) = y (lire : "f de x égale y")
On écrit aussi
:
f
: x 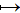 y
(lire : application f de E dans F") y
(lire : application f de E dans F")
Si f est une
application et x  E
et y E
et y  F sont tels
que f(x) = y : F sont tels
que f(x) = y :
x
est l'argument (ou la variable) de f, et l'antécédent
de y;
f(x), c'est-à-dire
y,
est l'image de x par f (ou la valeur
de f en x).
On dit encore que
f applique E dans F.
Dans le cas d'une relation
fonctionnelle au sens large, on peut définir l'ensemble de définition
ou domaine de définition Df de cette
relation comme le sous-ensemble des éléments de l'ensemble de
départ E qui ont une image dans l'ensemble d'arrivée F. Dans le cas d'une
application (fonction), telle qu'on vient de la d√©finir (o√Ļ tout x de
E a une image dans F), c'est l'ensemble de départ tout entier qui prend
le nom de domaine de définition de l'application.
 Quand
f
ne s'applique qu'à une seule variable, comme on l'a vu jusqu'ici,
f
est une fonction à une variable. Mais on peut aussi envisager des fonctions
s'appliquant à des n-uplets. On a alors affaire à des fonctions à n
variables. Quand
f
ne s'applique qu'à une seule variable, comme on l'a vu jusqu'ici,
f
est une fonction à une variable. Mais on peut aussi envisager des fonctions
s'appliquant à des n-uplets. On a alors affaire à des fonctions à n
variables.
 Quand
E = F , f est qualifiée d'autoapplication. Quand
E = F , f est qualifiée d'autoapplication.
 Si
une application f donne à tout élément x de E une unique image
b
dans F, f est qualifiée d'application
ou de fonction
constante. (Par exemple, quel que soit x, f (x) = 3). Si
une application f donne à tout élément x de E une unique image
b
dans F, f est qualifiée d'application
ou de fonction
constante. (Par exemple, quel que soit x, f (x) = 3).
 L'application
qui, dans E, associe à lui-même tout x (autrement dit L'application
qui, dans E, associe à lui-même tout x (autrement dit  x : f(x) = x) est appelée l'application identique ou identité
et est notée ordinairement IdE ou Id
(Id : x
x : f(x) = x) est appelée l'application identique ou identité
et est notée ordinairement IdE ou Id
(Id : x 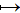 x ou Id(x) = x).
x ou Id(x) = x).
 G
étant un sous-ensemble de E et f une applications de E dans F,
l'application g telle que pour tout x appartenant à G on
a g(x) = f (x) est appelée la restriction de f à G, tandis
que f prendra le nom de prolongement de
g. G
étant un sous-ensemble de E et f une applications de E dans F,
l'application g telle que pour tout x appartenant à G on
a g(x) = f (x) est appelée la restriction de f à G, tandis
que f prendra le nom de prolongement de
g.
Composition
d'applications.
Considérons une application f
de E dans F (f : x 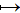 y ou f(x) = y) et une application g de F dans G (g
: y
y ou f(x) = y) et une application g de F dans G (g
: y  z ou g(y)
= z). Sous certaines conditions, il est possible de définir une
troisième application, disons h, qui fait correspondre directement
z à x (h : x z ou g(y)
= z). Sous certaines conditions, il est possible de définir une
troisième application, disons h, qui fait correspondre directement
z à x (h : x  z), autrement dit h(x) = f(g(x)) = z. Cette application prend le
nom d'application composée de f et de g. On la note communément
f o g (lire : "f rond g"); f o
g (x) = f (g(x)).
z), autrement dit h(x) = f(g(x)) = z. Cette application prend le
nom d'application composée de f et de g. On la note communément
f o g (lire : "f rond g"); f o
g (x) = f (g(x)).
 Une
application f d'un ensemble E dans lui-même peut être composée avec
elle-même. On note alors f² = f o f. Si f est composée
n
fois avec elle-même on écrit fn = f o
f o f... o f (n fois)
et l'on lconvient que f¬į correspond √† l'application identique dans E,
IdE : f¬į = IdE, soit f¬į (x)
= x. Une
application f d'un ensemble E dans lui-même peut être composée avec
elle-même. On note alors f² = f o f. Si f est composée
n
fois avec elle-même on écrit fn = f o
f o f... o f (n fois)
et l'on lconvient que f¬į correspond √† l'application identique dans E,
IdE : f¬į = IdE, soit f¬į (x)
= x.
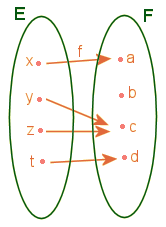
Diagramme
sagittal d'une application.
Le diagramme sagittal
d'une application est tel que, de tout élément de E, part une flèche
au
plus, aboutissant à un élément de F. Les éléments de F peuvent
en revanche être la destination de plusieurs flèches, ou d'aucune.
-
 |
Diagramme
sagittal d'une application. - Tous les éléments de l'ensemble de
départ E ont une image et une seule dans l'ensemble d'arrivée F par l'application
f. Certains éléments de l'ensemble de départ peuvent avoir plusieurs
images. Certains éléments de l'ensemble d'arrivée peuvent ne pas avoir
d'antécédent dans l'ensemble de départ. |
Types d'applications.
Injection.
Une application
f
de E dans F est injective (ou encore f est une injection),
si et seulement si, quels que que soient x et x' appartenant à E,
l'égalité de f(x) et de f(x') implique que x égale x' :
 x, x'
x, x'  E : f(x) = f(x') E : f(x) = f(x')  x = x'
x = x'
Application
injective.
Deux
éléments distincts
ont
des images distinctes.
De même, si
f'est
une injection, la diff√©rence de x et x' entra√ģne la diff√©rence de f(x)
et de f(x') :
 x, x'
x, x'  E : f(x) E : f(x) 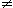 f(x')
f(x') 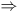 x x 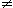 x'
x'
Surjection.
Une application
f
de E dans F est exhaustive ou surjective (ou
f est
une surjection), si et seulement si tous les éléments de F sont
les images par f des éléments de E. On dit que f'transforme
E en F.
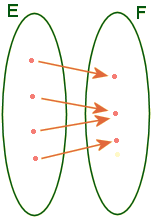
Application
surjective.
Tous
les éléments de l'ensemble
d'arrivée
ont au moins un antécédent.
Bijection.
Une application
f
de E dans F est biunivoque ou bijective (ou encore f
est une bijection) si f est à la fois injective et surjective.
Tout élément de l'ensemble image est l'image d'un unique élément de
l'ensemble de départ.
-
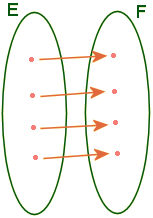
Application
bijective.
Tout
élément de l'ensemble d'arrivée
est
l'image d'un seul élément
de
l'ensemble de départ.
 Si
f
est une bijection de E dans F, il existe une application de F dans E qui
à chaque image d'un élément de F fait correspondre son antécédent
unique par f dans E. Cette fonction est appellée
application réciproque
de f et est notée f
-1. Si
f
est une bijection de E dans F, il existe une application de F dans E qui
à chaque image d'un élément de F fait correspondre son antécédent
unique par f dans E. Cette fonction est appellée
application réciproque
de f et est notée f
-1.
 Lorsqu'une bijection f est définie d'un ensemble E sur lui-même, ont
dit que f est une permutation; une permutation qui affecte seulement
deux éléments de E (f se comportant alors comme l'application
identique pour les autres éléments) on lui donne le nom de
transposition.
Lorsqu'une bijection f est définie d'un ensemble E sur lui-même, ont
dit que f est une permutation; une permutation qui affecte seulement
deux éléments de E (f se comportant alors comme l'application
identique pour les autres éléments) on lui donne le nom de
transposition.
Equipotence. Cardinal
d'un ensemble.
Ensembles
équipotents.
Lorsqu'une bijection peut être établie
entre deux ensembles, on dit que ces ensembles sont équipotents.
Tous les ensembles équipotents à un ensemble E forment une classe d'équivalence
à laquelle il est possible d'associer une entité mathématiques appelée
le cardinal de E et notée Card (E). Tous les ensembles équipotents
ont le même cardinal.
Cardinal
d'un ensemble.
Dans le cas des ensembles qui ont un nombre
fini d'éléments, le point commun, qui permet de définir l'équipotence
entre deux ensembles est le nombre de leurs éléments. On convient dès
lors de dire que si E possède n éléments, le cardinal de E sera n :
Card (E) = n.
 Si
E et F sont deux ensembles finis : Si
E et F sont deux ensembles finis :
Card (E) 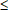 Card (F)
Card (F) 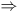 E
E 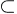 F. F.
Card (E X
F) = Card (E) . Card (F) (ou "X"
correspond au produit cartésien et "." à la multiplication entre
entiers).
 Si
F est une partie (sous-ensemble) d'un ensemble fini E : Si
F est une partie (sous-ensemble) d'un ensemble fini E :
Card (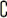 EF)
= Card (E) - Card (F). EF)
= Card (E) - Card (F).
Ensembles
infinis et nombres transfinis.
Cependant des bijections (relations d'équipotence)
peuvent aussi être définies entre ensembles infinis. Dans ce cas, des
notations nouvelles ont d√Ľ √™tre introduites pour parler des cardinaux
de ces ensembles (notamment pour les comparer). On utilise depuis Cantor
la lettre de l'alphabet h√©bra√Įque 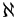 (aleph) munie d'un indice. L'ensemble
(aleph) munie d'un indice. L'ensemble 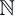 des entiers positifs aura ainsi pour cardinal
des entiers positifs aura ainsi pour cardinal 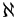 0
(lire
: aleph-zéro) et l'on dira que tout ensemble de cardinal 0
(lire
: aleph-zéro) et l'on dira que tout ensemble de cardinal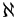 0
a la puissance du dénombrable; 0
a la puissance du dénombrable; 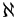 1
(aleph-1) est défini comme le cardinal de 1
(aleph-1) est défini comme le cardinal de 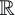 ,
ensemble des nombres réels, et l'on dira que tout ensemble de cardinal ,
ensemble des nombres réels, et l'on dira que tout ensemble de cardinal  1
a la puissance du continu. Les cardinaux des ensembles infinis sont
appelés nombres transfinis. 1
a la puissance du continu. Les cardinaux des ensembles infinis sont
appelés nombres transfinis.
Lois
de composition (opérations)
Jusqu'ici, on a défini une application comme
une mise en correspondance d'un élément x d'un ensemble quelconque E
avec un élément y d'un ensemble F. C'est ce qu'exprime l'écriture
f(x) = y, o√Ļ x  y et
y y et
y  F. F.
Une loi de composition ou opération
est une application dans laquelle l'ensemble de départ est un produit
cartésien. On considère alors la mise en correspondance d'un couple d'éléments
appartenant à un sous-ensemble G de l'ensemble produit E X
F avec un élément z appartenant à un ensemble H.
Si l'on continue d'adopter la même écriture
que précédemment, on aura : f (x,y) = z, avec (x, y)  G ou encore : f : (x, y)
G ou encore : f : (x, y) 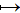 z. Mais ici encore, un changement d'écriture peut faciliter les
choses, ne serait-ce que parce que la nouvelle écriture sera plus conforme
aux usages déjà en vigueur pour exprimer certains lois de composition
courantes. Une loi de composition abandonnera donc le f pour le
remplacer par une autre symbole, tel que
z. Mais ici encore, un changement d'écriture peut faciliter les
choses, ne serait-ce que parce que la nouvelle écriture sera plus conforme
aux usages déjà en vigueur pour exprimer certains lois de composition
courantes. Une loi de composition abandonnera donc le f pour le
remplacer par une autre symbole, tel que  ou
ou  , et, plut√īt
que d'√©crire f (x, y) = z, on √©crira, par exemple : , et, plut√īt
que d'écrire f (x, y) = z, on écrira, par exemple :
x  y = z.
y = z.
On dira aussi que  est une opération sur l'ensemble considéré, le symbole
est une opération sur l'ensemble considéré, le symbole  représentant l'opérateur; x et y sont les termes de l'opération;
z est le composé de x et y.
représentant l'opérateur; x et y sont les termes de l'opération;
z est le composé de x et y.
 Le
symbole Le
symbole se lit "étoile".
Le symbole se lit "étoile".
Le symbole  se
prononce"truc". Le symbole se
prononce"truc". Le symbole  ,
qu'on rencontrera plus bas, se lit "antitruc". ,
qu'on rencontrera plus bas, se lit "antitruc".
 Les
quatre opérations arithmétiques, l'addition, la soustraction, la multiplication
et la division (symbolisées par les opérateurs +, -, x et
/ ), sont des lois de composition entre nombres. Dans le cas de l'addition
le composé est la somme des termes; dans le cas de la soustraction,
c'est la différence. Dans le cas de la multiplication, les termes
prennent le nom de facteurs; le composé celui de produit;
dans le cas de la division, le premier terme est le numérateur,
et le second le dénominateur, le composé est le quotient. Les
quatre opérations arithmétiques, l'addition, la soustraction, la multiplication
et la division (symbolisées par les opérateurs +, -, x et
/ ), sont des lois de composition entre nombres. Dans le cas de l'addition
le composé est la somme des termes; dans le cas de la soustraction,
c'est la différence. Dans le cas de la multiplication, les termes
prennent le nom de facteurs; le composé celui de produit;
dans le cas de la division, le premier terme est le numérateur,
et le second le dénominateur, le composé est le quotient.
 La
composition d'applications évoquée plus haut fournit un autre exemple
de loi de composition; elle est symbolisée par l'opérateur
o. La
composition d'applications évoquée plus haut fournit un autre exemple
de loi de composition; elle est symbolisée par l'opérateur
o.
Lois
de composition interne.
Une loi de composition
interne  définie sur E est une application d'une partie G de l'ensemble E
X
E dans E.
définie sur E est une application d'une partie G de l'ensemble E
X
E dans E.
On dit que E est
un ensemble fermé (clos, stable) par rapport à la loi (ou pour
la loi)  , ou
encore que E est muni de la loi ' , ou
encore que E est muni de la loi ' ou structuré par elle; ce que l'on écrit sous la forme : (E,
ou structuré par elle; ce que l'on écrit sous la forme : (E,  ),
o√Ļ E prend le nom de support de la structure. ),
o√Ļ E prend le nom de support de la structure.
 De
la même façon, un sous-ensemble non vide F de l'ensemble E est dit stable
pour la loi De
la même façon, un sous-ensemble non vide F de l'ensemble E est dit stable
pour la loi  si pour tous les éléments x, y de F, on a : x
si pour tous les éléments x, y de F, on a : x  y
y  F. Autrement dit,
F est stable pour la loi F. Autrement dit,
F est stable pour la loi  (en toute rigueur, pour la restriction de
(en toute rigueur, pour la restriction de  dans F) si
dans F) si  est
aussi une loi de composition interne dans F. est
aussi une loi de composition interne dans F.
Lois
de composition externe.
La notion de loi
de composition externe invite à considérer deux ensembles distincts
E et F et une loi de composition  .
Cette loi est une loi de composition externe si elle est une application
de E X F dans F : ( .
Cette loi est une loi de composition externe si elle est une application
de E X F dans F : ( (x, y)
(x, y)  E X
F : x E X
F : x  y = z
y = z  F). F).
 x x  y s'appelle le composé (ou le produit) de x et de y pour
la loi
y s'appelle le composé (ou le produit) de x et de y pour
la loi  ; ;
 Les
éléments de E sont appelées opérateurs et E est qualifié d'ensemble
des opérateurs de la loi Les
éléments de E sont appelées opérateurs et E est qualifié d'ensemble
des opérateurs de la loi  . .
 Soit
G un sous-ensemble non vide de F; G est dit stable pour la loi externe Soit
G un sous-ensemble non vide de F; G est dit stable pour la loi externe  si pour tout élément x de l'ensemble d'opérateurs E et pour tout élément
y de F, leur produit appartient à F.
si pour tout élément x de l'ensemble d'opérateurs E et pour tout élément
y de F, leur produit appartient à F.
 Si
E = F, on retrouve bien s√Ľr une loi de composition interne (une loi de
composition interne est un cas particulier de loi de composition externe). Si
E = F, on retrouve bien s√Ľr une loi de composition interne (une loi de
composition interne est un cas particulier de loi de composition externe).
La fécondité de ces
notions commence √† appara√ģtre lorsque, de surcro√ģt, F est muni d'une
loi de composition interne  .
On pourra former, par exemple des expressions du genre x .
On pourra former, par exemple des expressions du genre x  y = z
y = z  t, et
d'autres plus compliquées (V. ci-dessous). t, et
d'autres plus compliquées (V. ci-dessous).
Propriétés des
lois de composition.
Commutativité.
Une loi de composition
interne  dans
E est commutative si si pour tout x et tout y
on a : x dans
E est commutative si si pour tout x et tout y
on a : x  y =
y y =
y  x. x.
 La
notion de commutativité, définie ici pour des éléments d'un ensemble
peut s'étendre, à la réunion de deux ensembles
: E U F = F U E; même chose pour l'intersection : E La
notion de commutativité, définie ici pour des éléments d'un ensemble
peut s'étendre, à la réunion de deux ensembles
: E U F = F U E; même chose pour l'intersection : E  F = F
F = F  E. E.
Associativité.
Une loi de composition
interne  dans
E est associative si si pour tout x, tout y
et tout z appartenant à E on a : x dans
E est associative si si pour tout x, tout y
et tout z appartenant à E on a : x  ( y
( y  z) = (x z) = (x  y)
y)  z. z.
 La
réunion deux ensembles est associative : (E U F) U G = E U (F U
G); même chose encore pour l'intersection (E La
réunion deux ensembles est associative : (E U F) U G = E U (F U
G); même chose encore pour l'intersection (E  F)
F)  G = E G = E  (F
(F  G) G)
 La
composition des applications o est également associative
: pour toute application f, g et h, on a : (f o
g) o h = f o (g
o h). La
composition des applications o est également associative
: pour toute application f, g et h, on a : (f o
g) o h = f o (g
o h).
Dans le cas d'une loi
de composition externe  ,
on dira qu'elle est associative par rapport à une loi de composition interne ,
on dira qu'elle est associative par rapport à une loi de composition interne  ,
si pour tout élément x de E, et tout élément (y, z) de F², ont peut
dire que : (y ,
si pour tout élément x de E, et tout élément (y, z) de F², ont peut
dire que : (y  z)
z)  x = y x = y (z
(z x). x).
Distributivité.
La distributivité
est une propriété qui implique une loi de composition externe  et une loi de composition interne
et une loi de composition interne  .
On dira que la loi .
On dira que la loi  est distributive par rapport à la loi interne
est distributive par rapport à la loi interne  de F si, pour tout x appartenant à F et tout couple (y, z) appartenant
à E², on a-:
x
de F si, pour tout x appartenant à F et tout couple (y, z) appartenant
à E², on a-:
x  (y (y  z) = (x
z) = (x y) y)  (x
(x z). z).
 Distributivité
de l'union et de l'intersection : la réunion est distributive par rapport
à l'intersection : E U (F Distributivité
de l'union et de l'intersection : la réunion est distributive par rapport
à l'intersection : E U (F  G) = (E U F)
G) = (E U F)  (E U G); et l'intersection est distributive par rapport à la réunion
: E
(E U G); et l'intersection est distributive par rapport à la réunion
: E  (F U G)
= (E (F U G)
= (E  F) U (E F) U (E  G).
G).
Un forme différente
de distributivité peut être définie en impliquant une loi de composition
externe  et
deux lois de composition internes et
deux lois de composition internes  et
et  (opérant
toutes deux dans un ensemble F). Pour tout x appartenant à E et pour tout
u, v appartenant à F, on devra avoir : (u (opérant
toutes deux dans un ensemble F). Pour tout x appartenant à E et pour tout
u, v appartenant à F, on devra avoir : (u  v)
v)  x = (u x = (u x) x)  (v
(v  x). x).
Eléments réguliers,
élément absorbant, élément neutre.
Certains éléments
d'un ensemble peuvent révéler des propriétés particulières lorsqu'opère
sur eux une loi de composition. (Nous considérerons dans ce qui suit un
ensemble E muni d'une loi de composition  interne).
interne).
Eléments
réguliers.
Lorsque a  x = a
x = a  y
y 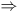 x = y,
a est un élément régulier à gauche; c'est un élément régulier
à droite lorsque x x = y,
a est un élément régulier à gauche; c'est un élément régulier
à droite lorsque x  a = y
a = y  a a 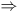 x = y; enfin a un élément régulier tout court s'il est régulier
à droite et régulier à gauche.
x = y; enfin a un élément régulier tout court s'il est régulier
à droite et régulier à gauche.
 On
appelle simplification le passage de l'équation x On
appelle simplification le passage de l'équation x  a = y
a = y  a
(ou a a
(ou a  x = a x = a  y) à l'équation x = y : c'est ce que l'on fait couramment en algèbre
lorsque, par exemple, ayant l'équation 2.(x+3) = 2.(y-5), on passe "en
simplifiant" à l'équation x+3 = y-5.
y) à l'équation x = y : c'est ce que l'on fait couramment en algèbre
lorsque, par exemple, ayant l'équation 2.(x+3) = 2.(y-5), on passe "en
simplifiant" à l'équation x+3 = y-5.
Elément
absorbant.
On dit que a
est un élément absorbant si pour tout y de E, on a
a  y = y
y = y  a = a. a = a.
 Dans
( Dans
( , x),
soit dans l'ensemble des entiers naturels muni de la multiplication, l'élément
absorbant est 0, car quel que soit le nombre n lorsqu'il est multiplié
par 0 le résultat est zéro : n x 0 = 0. , x),
soit dans l'ensemble des entiers naturels muni de la multiplication, l'élément
absorbant est 0, car quel que soit le nombre n lorsqu'il est multiplié
par 0 le résultat est zéro : n x 0 = 0.
 L'ensemble
vide joue le r√īle d'√©l√©ment absorbant pour l'intersection : pour tout
ensemble E, E L'ensemble
vide joue le r√īle d'√©l√©ment absorbant pour l'intersection : pour tout
ensemble E, E  ' '  =
= 
Elément
neutre.
De même, si pour
tout x de E, il existe un élément e de E tel que e  x = x, on appelle e élément neutre à gauche; si on a la
relation x
x = x, on appelle e élément neutre à gauche; si on a la
relation x  e
= x, e est l'√©l√©ment neutre √† droite. Il est bien s√Ľr possible
aussi que x e
= x, e est l'√©l√©ment neutre √† droite. Il est bien s√Ľr possible
aussi que x  e = e
e = e  x = x;
dans ce cas, e est l'élément neutre à droite et à gauche (ou
l'élément neutre tout court). x = x;
dans ce cas, e est l'élément neutre à droite et à gauche (ou
l'élément neutre tout court).
 Lorsqu'un
ensemble E possède un élément neutre pour une loi Lorsqu'un
ensemble E possède un élément neutre pour une loi  ,
on note souvent E* , l'ensemble E auquel on a √īt√© l'√©l√©ment neutre
(E* = E - {e}). Il faut cependant qu'aucune confusion ne soit à craindre
sur l'identité de l'élément neutre et de la loi de composition concernée. ,
on note souvent E* , l'ensemble E auquel on a √īt√© l'√©l√©ment neutre
(E* = E - {e}). Il faut cependant qu'aucune confusion ne soit à craindre
sur l'identité de l'élément neutre et de la loi de composition concernée.
 Dans
( Dans
( , +),
c'est-à-dire dans l'ensemble des entiers naturels muni de l'addition,
l'élément neutre est 0, car quelque soit le nombre n lorsque il ajouté
à 0 le résultat est n + 0 = 0 + n = n. , +),
c'est-à-dire dans l'ensemble des entiers naturels muni de l'addition,
l'élément neutre est 0, car quelque soit le nombre n lorsque il ajouté
à 0 le résultat est n + 0 = 0 + n = n.
 Dans
( Dans
( , x),
c'est-à-dire dans l'ensemble des entiers naturels muni de la multiplication,
l'élément neutre est 1, car quelque soit le nombre n lorsque il multiplié
par 1 le résultat est n x 1 = 1 x n = n. , x),
c'est-à-dire dans l'ensemble des entiers naturels muni de la multiplication,
l'élément neutre est 1, car quelque soit le nombre n lorsque il multiplié
par 1 le résultat est n x 1 = 1 x n = n.
 L'ensemble
vide joue le r√īle d'√©l√©ment neutre pour la r√©union : pour tout ensemble
E, E L'ensemble
vide joue le r√īle d'√©l√©ment neutre pour la r√©union : pour tout ensemble
E, E  '' '' = E.
= E.
Eléments
symétrisables et symétriques.
Un élément x est
dit symétrisable pour la loi  s'il existe un élément x' tel que :
s'il existe un élément x' tel que :
x  x' = x'
x' = x'  x =
e (e étant l'élément neutre). L'élément x' est appelé le symétrique
(ou l'inverse) de x dans (E, x =
e (e étant l'élément neutre). L'élément x' est appelé le symétrique
(ou l'inverse) de x dans (E,  ). ).
 Dans
( Dans
(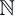 , +),
aucun élément, sauf 0, n'a de symétrique. En revanche, tous les éléments
de , +),
aucun élément, sauf 0, n'a de symétrique. En revanche, tous les éléments
de 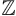 tous les éléments sont symétrisables pour l'addition : le symétrique
prend ici le nom d'opposé ( -n est l'opposé de n
pour l'addition).
tous les éléments sont symétrisables pour l'addition : le symétrique
prend ici le nom d'opposé ( -n est l'opposé de n
pour l'addition).
 Dans
( Dans
( , x),
aucun élément, sauf 1 et -1, n'a de symétrique. En revanche, tous les
éléments de , x),
aucun élément, sauf 1 et -1, n'a de symétrique. En revanche, tous les
éléments de  ,
sauf 0, sont symétrisables pour la multiplication (1/n est le symétrique
ou l'inverse de n pour la multiplication). ,
sauf 0, sont symétrisables pour la multiplication (1/n est le symétrique
ou l'inverse de n pour la multiplication).
Homomorphismes.
Une application f quelconque définie
entre de deux ensembles (E,  )
et (F, )
et (F,  )
munis chacun d'une loi de composition est un homomorphisme lorsque
pour tout x et y appartenant à E, on vérifie l'égalité : f (x )
munis chacun d'une loi de composition est un homomorphisme lorsque
pour tout x et y appartenant à E, on vérifie l'égalité : f (x  y) = f(x)
y) = f(x)  f(y).
f(y).
Homomorphisme est un terme général. Les
homomorphismes portent des noms particuliers selon que l'application est
bijective ou non, ou selon que E est différent de F ou non.
Isomorphisme.
Lorsque les deux
ensembles E et F sont différents, que l'application f est un homomorphisme
de (E,  ) dans
(F, ) dans
(F,  ) et que
f
est de surcro√ģt bijective de E dans F : on dit que f est un isomorphisme
de (E, ) et que
f
est de surcro√ģt bijective de E dans F : on dit que f est un isomorphisme
de (E,  ) dans (F,
) dans (F,  ) )
Endomorphisme.
Lorsqu'on ne considère
qu'un seul ensemble E, qu'une seule loi de composition  ,
et que f, définie de E sur lui-même, est un homomorphisme ( ,
et que f, définie de E sur lui-même, est un homomorphisme ( x, y
x, y  E et f(x) E et f(x)  E : f (x
E : f (x  y) = f(x)
y) = f(x)  f(y))
: on dit que f est un endomorphisme de (E, f(y))
: on dit que f est un endomorphisme de (E,  ). ).
Automorphisme.
Un automorphisme
répond à la même situation que dans le cas de de l'endomorphisme, sauf
que maintenant il est demand√© √† f d'√™tre de surcro√ģt bijective
: on dit que alors f est un automorphisme de (E, ). ).
Structures algébriques.
Les ensembles non
vides munis d'une ou de plusieurs lois de composition peuvent avoir des
propriétés particulières que l'on peut retrouver aussi dans d'autres
ensembles munis d'autres lois. On dit que ces ensembles munis de leurs
lois de composition respectives partagent la même structure, dite structure
algébrique.
Certaines de ces
structures, d'usage courant en mathématiques, portent des noms. Telles
sont, par exemple, les structures algébriques suivantes :
Groupe.
(E, )
est un groupe ou possède une structure de groupe si et seulement
si : )
est un groupe ou possède une structure de groupe si et seulement
si :
1¬į) La
loi  est associative
( est associative
( x, y z x, y z  E : x
E : x  (y (y  z) = (x
z) = (x  y) y)  z) ;
z) ;
2¬į) il existe dans
E un élément neutre e (à gauche et à droite) pour la loi
de composition  (
(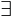 e | e |  x
: x x
: x  e = x et
e e = x et
e  x = x) ; x = x) ;
3¬į) chaque √©l√©ment
possède son symétrique ( x
: x
: 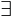 x' | x x' | x  x' = e).
x' = e).
Si, de plus,  est commutative, (E,
est commutative, (E,  )
sera appelé groupe commutatif ou groupe abélien. )
sera appelé groupe commutatif ou groupe abélien.
Un sous-ensemble
non vide F de E muni d'une loi  est un sous-groupe de (E,
est un sous-groupe de (E,  ),
pour le dire sommairement, si et seulement si (F, ),
pour le dire sommairement, si et seulement si (F,  )
est un groupe. Si l'on veut être plus explicite, on dira que (F, )
est un groupe. Si l'on veut être plus explicite, on dira que (F,  )
est un sous groupe de (E, )
est un sous groupe de (E,  ),
si et seulement F est stable pour la loi ),
si et seulement F est stable pour la loi  et si le restriction à F de la loi
et si le restriction à F de la loi  (encore notée
(encore notée  )
munit F d'une structure de groupe. )
munit F d'une structure de groupe.
Anneau.
Soit (E,  , ,  )
l'ensemble E muni des lois de composition interne )
l'ensemble E muni des lois de composition interne  et
et  , on dira
que E ( , on dira
que E ( , ,  )
est un anneau si et seulement si : )
est un anneau si et seulement si :
1¬į) (E,  )
est un groupe commutatif; )
est un groupe commutatif;
2¬į) la loi  est associative dans E;
est associative dans E;
3¬į) la loi  est distributive par rapport √† la loi de composition
est distributive par rapport à la loi de composition  dans E.
dans E.
S'il existe dans E un
élément neutre pour la loi  .
Cet élément est appelé unité de l'anneau, et l'anneau est dit
d'anneau unitaire. .
Cet élément est appelé unité de l'anneau, et l'anneau est dit
d'anneau unitaire.
Si la loi  est commutative dans E, on a affaire à un anneau commutatif.
est commutative dans E, on a affaire à un anneau commutatif.
F étant un sous-ensemble
non vide de l'ensemble E, on dira que (F,  , ,  )
est un sous-anneau de (E, )
est un sous-anneau de (E,  , ,  )
si et seulement si F est stable pour les deux lois )
si et seulement si F est stable pour les deux lois  et
et  ,
et si ces lois (ou plus précisément leurs restrictions) munissent
F s'une structure d'anneau. ,
et si ces lois (ou plus précisément leurs restrictions) munissent
F s'une structure d'anneau.
Corps.
Si et
et  sont deux
lois de composition interne définies sur E, (E, sont deux
lois de composition interne définies sur E, (E,  , ,  )
est un corps si et seulement si : )
est un corps si et seulement si :
1¬į)
(E,  )
est un groupe abélien; )
est un groupe abélien;
2¬į) (E,  )
est un groupe; )
est un groupe;
3¬į) La loi  est distributive par rapport √† la loi
est distributive par rapport à la loi  dans E.
dans E.
Autrement dit, (E,  , ,  )
est un corps si et seulement si (E, )
est un corps si et seulement si (E,  , ,  )
est un anneau unitaire dans lequel tout élément différent de l'élément
neutre pour la loi )
est un anneau unitaire dans lequel tout élément différent de l'élément
neutre pour la loi  a un symétrique pour la loi
a un symétrique pour la loi  . .
On parle de corps commutatif lorsque la
loi  est commutative. est commutative.
Etant donné une
sous-ensemble non-vide F de l'ensemble E, des conditions analogues à celles
qui ont permis de définir la structure de sous-anneau sont nécessaires
pour définir la structure de sous-corps : (F,  , ,  )
est un sous-corps de (E, )
est un sous-corps de (E,  , ,  )
si et seulement si F est stable pour )
si et seulement si F est stable pour  et si (F,
et si (F,  , ,  )
a une structure de corps. )
a une structure de corps.
Espace
vectoriel.
On dit que (E,  ,
‚ÄĘ) un espace vectoriel sur (F, ,
‚ÄĘ) un espace vectoriel sur (F,  , ,  )
si et seulement si : )
si et seulement si :
1¬į) La
loi  est une
loi de composition interne dans E telle que (E, est une
loi de composition interne dans E telle que (E,  )
soit un groupe abélien; les éléments de E sont appelés
vecteurs. )
soit un groupe abélien; les éléments de E sont appelés
vecteurs.
2¬į) Les deux lois  et
et  dotent
F d'une structure de corps commutatif; les éléments de F sont appelés
scalaires. dotent
F d'une structure de corps commutatif; les éléments de F sont appelés
scalaires.
3¬į) La loi de composition
externe ‚ÄĘ d√©finie dans F x E v√©rifie les quatre propri√©t√©s suivantes
pour tout scalaire x, y et pour tout vecteur u, v-
:
x ‚ÄĘ (y
‚ÄĘ u) = (x  y) ‚ÄĘ u
y) ‚ÄĘ u
(x  y) ‚ÄĘ u = (x ‚ÄĘ u)
y) ‚ÄĘ u = (x ‚ÄĘ u)  (y ‚ÄĘ u)
(y ‚ÄĘ u)
x ‚ÄĘ (u  v) = (x ‚ÄĘ u)
v) = (x ‚ÄĘ u)  (x ‚ÄĘ v)
(x ‚ÄĘ v)
il existe
dans F un élément neutre e pour la loi de composition externe
‚ÄĘ (pour tout v appartenant √† E, e ‚ÄĘ v = v ‚ÄĘ e = v).
G, sous ensemble de
E, est un sous-espace vectoriel d'un espace vectoriel (E,  ,
‚ÄĘ) sur un corps commutatif (F, ,
‚ÄĘ) sur un corps commutatif (F,  , ,  )
si et seulement si : 1¬į) G est stable pour les lois )
si et seulement si : 1¬į) G est stable pour les lois  dans E et ‚ÄĘ dans E; 2¬į les restrictions √† G de ces deux lois munissent
G d'une structure d'espace vectoriel sur F.
dans E et ‚ÄĘ dans E; 2¬į les restrictions √† G de ces deux lois munissent
G d'une structure d'espace vectoriel sur F.
 La
branche des mathématiques qui étudie les espaces vectoriels s'appelle
l'algèbre linéaire, en référence à certaines applications,
appelées applications linéaires, dont l'étude y occupe une place
importante : f est une application linéaire de E sur le corps F
si elle vérifie l'égalité : La
branche des mathématiques qui étudie les espaces vectoriels s'appelle
l'algèbre linéaire, en référence à certaines applications,
appelées applications linéaires, dont l'étude y occupe une place
importante : f est une application linéaire de E sur le corps F
si elle vérifie l'égalité :
f (x ‚ÄĘu  y ‚ÄĘ v) = x ‚ÄĘ f(u)
y ‚ÄĘ v) = x ‚ÄĘ f(u)  y ‚ÄĘ f(v).
y ‚ÄĘ f(v).
 On
nomme dual algébrique de E l'ensemble de toutes les applications
de E dans F, et on le note E* (attention à ne pas confondre cette écriture
avec celle employée notamment pour nommer les ensembles de nombres auxquels
on a √īt√© le z√©ro). On
nomme dual algébrique de E l'ensemble de toutes les applications
de E dans F, et on le note E* (attention à ne pas confondre cette écriture
avec celle employée notamment pour nommer les ensembles de nombres auxquels
on a √īt√© le z√©ro).
 Un
espace vectoriel (E, Un
espace vectoriel (E,  ,
‚ÄĘ) sur (F, ,
‚ÄĘ) sur (F,  , ,  )
peut aussi impliquer d'autres lois de composition. Un exemple, d'usage
très courant lorsqu'on étudie les vecteurs sur ( )
peut aussi impliquer d'autres lois de composition. Un exemple, d'usage
très courant lorsqu'on étudie les vecteurs sur (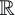 ,
+ x) en est fourni par le produit scalaire (notons-le "."
) entre deux vecteurs u et v, et dont le composé k est un scalaire (u.v
= k). Cette loi ne répond ni à la définition d'une loi de composition
interne, ni à celle d'une loi de composition externe. ,
+ x) en est fourni par le produit scalaire (notons-le "."
) entre deux vecteurs u et v, et dont le composé k est un scalaire (u.v
= k). Cette loi ne répond ni à la définition d'une loi de composition
interne, ni à celle d'une loi de composition externe.
Un certain nombre d'autres structures algébriques
ont √©t√© d√©finies et portent un nom : mono√Įdes, modules, alg√®bres,
etc. Des ensembles munis d'une structure algébrique peuvent être munis
en même temps d'une structure d'un autre type (par exemple , les groupes
de Lie, associent à la structure algébrique de groupe une structure
géométrique; l'ensemble des entiers relatifs 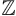 peut être muni en même temps d'une structure algébrique d'anneau, par
l'addition (+) et la multiplication (x), et d'une structure d'ordre total
(par la relation
peut être muni en même temps d'une structure algébrique d'anneau, par
l'addition (+) et la multiplication (x), et d'une structure d'ordre total
(par la relation 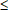 ),
etc. ),
etc. |
|









