Figures magiques

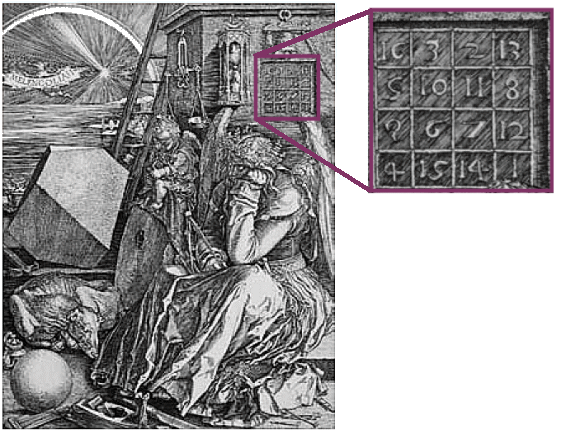
Un carré magique dans la gravure de Dürer intitulée Mélancolie (1514).

On s'est souvent proposé ainsi des problèmes analogues de magie littérale, ou les nombres sont remplacés par des lettres devant satisfaire à certaines conditions. On considère parfois aussi des cercles magiques, des triangles magiques, etc.; mais c'est surtout sur le carrés que se sont portées les recherches.

Carrés magiques et diaboliques. On appelle carré magique un carré divisé en d'autres plus petits au moyen de parallèles à ses côtés. Dans chacun des petits carrés est inscrit un nombre entier. Ces nombres entiers doivent être en progression arithmétique (mais au point de vue mathématique, il est clair que l'on peut faire abstraction de cette condition). Le carré magique doit jouir de cette propriété que la somme des nombres placés dans une même rangée horizontale, ou dans une même rangée verticale, ou dans une même diagonale, soit toujours la même. La recherche des nombres à inscrire dans les cases d'un carré magique est évidemment un problème d'analyse indéterminée du premier degré. Voici deux exemples de carrés magiques empruntés aux Récréations mathématiques de Lucas.
-
 

8	1	6
3	5	7
4	9	2

La somme des nombres écrits dans une même rangée ou dans une même diagonale est 15 et le carré magique précédent contient les 9 premiers nombres.
-

15	6	9	4
10	3	16	5
8	13	2	11
1	12	7	14

La somme des nombres écrits dans une même rangée ou dans une même diagonale est 34. Lorsqu'un carré magique est tel qu'en le coupant en deux par une parallèle à un côté et en permutant les deux morceaux on forme un nouveau carré magique, on dit que le carré est Diabolique; le carré précédent est diabolique, comme on peut s'en assurer. 

Les carrés magiques étaient connus de toute antiquité, les anciens leur attribuaient des propriétés merveilleuses. D'illustres mathématiciens n'ont pas dédaigné de s'occuper de la construction des carrés magiques ; parmi eux il convient de citer Emmanuel Moscopule, Cardan, Stiefel, Bachet, Fermat, Euler, etc. (A. L. / H. Laurent).

J. Sesiano, Les carrés magiques dans les pays de l'Islam, Presses polytechniques et universitaires romandes, 2004. - L'une des contributions scientifiques les plus originales du monde musulman est sans doute le développement de méthodes générales de construction des carrés magiques, permettant de remplir un carré ayant un nombre carré de cases par une suite de nombres naturels différents de telle sorte que la somme dans chacune des lignes et des colonnes, ainsi que dans chacune des deux diagonales principales, soit la même. A partir de textes du Xe siècle et du Moyen Age, l'auteur, historien des mathématiques, offre une synthèse complète et sans précédent sur la genèse et l¹usage des carrés magiques dans les pays musulmans.