Harriot

Thomas Harriot (1560-1621).

Harriot fut reconnaissant des bontés du duc; et il ne l'abandonna point pendant sa longue captivité à la Tour de Londres. Robert Hues et Walther Warner, pensionnés également par Percy, montrèrent un semblable dévouement, et le suivirent aussi à la Tour. Depuis ce temps, ces trois savants furent surnommés les trois mages du duc de Northumberland. Harriot mourut à Londres, le 2 juillet 1621, âgé de 60 ans et quelques mois, après avoir cruellement souffert d'un chancre à la lèvre, qu'on attribuait à l'habitude qu'il avait contractée de tenir à la bouche ses instrumenta de mathématique en cuivre souvent chargés de vert-de-gris. Ses amis lui firent élever un tombeau dans l'église St-Christophe.

Harriot était en correspondance avec plusieurs savants, entre autres Kepler, avec lequel il eut une discussion sur la théorie de l'arc-en-ciel. La relation de son Voyage en Virginie a été imprimée (en anglais). Londres, 1588, in-4°, et dans le Recueil d'Hakluyt; la traduction latine, par un anonyme, forme la première partie de la Collection des grands voyages.

L'ouvrage qui a fait la réputation de ThomasHarriot comme mathématicien est intitulé Arta analytica praxis ad equationes algebricae resoluendas, Londres, 1631, in-fol. Il y met parfaitement en lumière la nature et la formation des équations. Le premier il égale toute l'expression d'une équation à zéro. Ainsi, au lieu d'écrire x = b, on écrira x - b = 0; au lieu de x² - 20x = 9, on mettra x² - 20x - 9 = 0. Montucla (Histoire des mathématiques, t. 2, p.106), remarque qu'Harriot fut bien éloigné de faire tout l'usage qu'il pouvait de saut découverte et d'en sentir tout l'avantage, et qu'il n'eut qu'une idée peu développée des racines négatives. Le principal service qu'il ait rendu aux mathématiques, c'est d'avoir observé que toutes les équations d'ordres supérieurs sont des produits d'équations simples; découverte de laquelle découlent une foule de choses intéressantes pour l'analyse.

Prenons, par exemple, des équations, telles que x ± a = 0, x ± b = 0, x ± c = 0, et avec telle combinaison de signes que l'on voudra; par exemple, en multipliant ensemble 
x + a = 0, x - b = 0, x + c = 0, on obtiendra un produit qui a pour expression :

x³ + (a - b + c) x^² - (ab + bc - ac) x - abc = 0,

Ce qui précède conduit à une méthode générale pour résoudre non seulement les équations du troisième degré, mais celles d'un degré quelconque au-dessus. Puisque la quantité connue est le produit de toutes les racines de l'équation, si ces racines sont rationnelles et entières, elles seront nécessairement quelques-uns des diviseurs de ce produit. Il faudra donc essayer lequel d'entre eux, mis à la place de l'inconnue, positivement ou négativement, rendra l'équation égale à zéro. Si cela réussit, ce sera l'une des valeurs de l'inconnue. 

Exemple : que l'équation proposée soit x³-17 x²+79 x - 63=0. Les diviseurs de 63 sont 1, 3, 7,9, 21, 63; par conséquent, si une des racines de l'équation est un nombre entier, ce nombre sera l'un de ces diviseurs. En effet, si au lieu de x on met 1, ou 7, ou 9, tous les termes se détruiront. Les valeurs de l'inconnue seront donc 1, ou 7, ou 9, et l'équation sera divisible par x - 1, ou par x - 7, ou par x - 9. 

De même dans l'équation x³ - 34x - 45 = 0 les diviseurs de 45 sont 1, 3, 5, 9, 15, 45; en les essayant les uns après les autres, on trouve que -5 étant substitué à la place de x, l'équation se détruit. C'est pourquoi l'une des racines est -5, et, divisant cette équation par x + 5, on l'abaisse à celle-ci : x²-  5x - 9 = 0, dont les racines sont :

Si aucune de ces substitutions ne réussit, c'est un signe que la racine de l'équation n'est pas un nombre rationnel, ni entier.

Wallis a singulièrement grossi la liste des découvertes d'Harriot; mais la plupart de celles dont il lui fait honneur appartiennent incontestablement à Viète ou à Descartes, dont Wallis s'attache à rabaisser le génie pour relever celui de son compatriote. Montucla a réduit à leur juste valeur les services du mathématicien anglais; et ils sont assez grands pour lui mériter, dans un rang secondaire, une place parmi les hommes qui ont contribué aux progrès des sciences mathématiques.
-

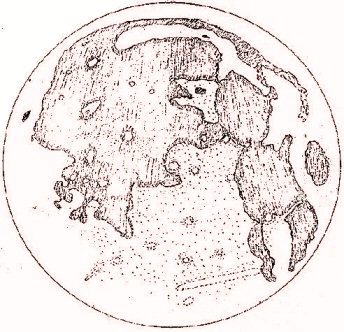
La Lune selon Thomas Harriot.
Source : The Galileo Project, page : Thomas Harriot's Moon Drawings.

On conserve un traité d'Harriot, intitulé Ephemeris chyrometrica, dans la bibliothèque du collège de Sion. Quelques autres de ses manuscrits ont été retrouvés en 1784, dans le château du duc de Northumberland, au comté de Sussex; et l'un d'eux prouve qu'Harriot s'était procuré un télescope batavique ou qu'il en avait deviné la construction, et qu'il concourut, avec Galilée, à la découverte des taches du Soleil. (W-s. / H.).