 | L'idée de nombre a son origine la plus naturelle dans la considération de plusieurs objets distincts. Si l'on considère des objets de même nature, l'un d'eux, pris pour terme de comparaison, est appelé unité. On entend par nombre l'unité ou plusieurs unités, ou, dit autrement, le résultat de la comparaison d'une grandeur quelconque à son unité. C'est par extension qu'on l'introduit dans la mesure de toutes les grandeurs. Si l'on dit, par exemple, quinze moutons et quinze kilogrammes, la relation de la grandeur à son unité est la même dans les deux cas, mais, dans le premier, l'idée est plus simple, parce que la séparation des unités est matérielle, tandis que dans le second elle est purement fictive. Quand un nombre est énoncé sans que l'on indique la nature des unités qu'il représente, on le nomme nombre abstrait; dans le cas contraire, il s'appelle nombre concret; ainsi 7 est un nombre abstrait, et quand on dit 7 litres, le nombre est concret. Nous mentionnons ces dénominations parce qu'on risque de les rencontrer dans les anciens ouvrages d'arithmétique, mais nous devons avertir que la seconde tend à donner une idée inexacte. Un nombre concret n'est pas un nombre, c'est une grandeur. Quand on dit 7 litres, le nombre est 7, le mot litre complète l'idée, mais ne la modifie pas. Les mots égaler, annoter ne peuvent pas être définis d'une manière générale, parce qu'ils ont trop de significations. Mais s'il est impossible de les définir d'une manière générale, il devient possible, et même il devient indispensable de les définir quand on les applique à des objets déterminés. Nous supposerons, dans la suite, que l'on ait, donné de ces mots des définitions qui ne dépendent que des propriétés communes à tous les objets auxquels ils s'appliquent. Ainsi, dans ces définitions, la nature des objets ne devra jouer aucun rôle; de plus, il sera bien entendu que ne rien ajouter à un de ces objets ce sera ne lui faire subir aucune modification. On appelle grandeurs mesurables ou quantités toutes les choses à propos desquelles on a défini les mots égaler, ajouter, en se conformant aux prescriptions précédentes, alors : « deux qualités égales à une autre sont égales entre elles », « le résultat obtenu en ajoutant plusieurs quantités est indépendant de l'ordre dans lequel on les ajoute », enfin, « quand on n'ajoute rien à une quantité on ne la modifie pas ». On dit qu'une quantité A est plus grande qu'une autre B (ou que B est plus petit que A), si l'on peut obtenir A en ajoutant à B une certaine quantité C. On dit que des quantités sont de même espèce, si l'on peut les concevoir égales, plus grandes ou plus petites les unes que les autres, et si l'on peut les ajouter entre elles. Le nombre qui mesure une quantité est une locution ou un signe qui sert à la représenter, à l'aide de laquelle on désigne cette quantité et toutes celles qui lui sont égales, de manière à les distinguer de toutes celles qui sont plus grandes ou plus petites (en termes mathématiques, on dira qu'on a affaire à des classes d'équivalence). Mesurer une quantité, c'est chercher le nombre qui la mesure. Montrons maintenant comment on peut former les nombres. (H. Laurent). Les ensembles de nombres Ensemble des nombres entiers naturels.
Considérons des quantités de même espèce, choisissons parmi ces quantités une quantité arbitraire que nous appellerons unité, nous dirons que l'unité et les quantités qui lui sont égales, et qui sont aussi des unités, sont mesurées par le nombre un; toutes les quantités égales du résultat de l'addition d'une unité avec une unité sont dites mesurées par le nombre deux; toutes les quantités égales au résultat de l'addition d'une unité avec, une quantité mesurée par le nombre deux sont dites mesurées par le nombre trois... On appelle nombres entiers ceux qui servent ainsi à mesurer les quantités résultant de l'addition de plusieurs unités. On peut concevoir que l'on ait donné un nom particulier à chacun de ces nombres, et qu'on l'ait représenté au moyen d'un signe particulier, c'est ce que la numération nous apprend à faire. L'ensemble des nombres des nombres entiers naturels, c'est-à-dire des nombres utilisés pour compter les objets est appelé  . Le zéro (0), qui, à strictement parler, ne sert pas à compter des objets puisqu'il exprime justement le fait qu'il n'y a a pas d'objet à compter, est aussi rangé dans l'ensemble des nombres entiers naturels. Ainsi : . Le zéro (0), qui, à strictement parler, ne sert pas à compter des objets puisqu'il exprime justement le fait qu'il n'y a a pas d'objet à compter, est aussi rangé dans l'ensemble des nombres entiers naturels. Ainsi :  = {0, 1, 2, 3, 4, ...} = {0, 1, 2, 3, 4, ...}
0 est le plus petit élément de  ; il n'y a pas de plus grand élément. De nombreux problèmes demandent de considérer l'ensemble des entiers naturels sans le zéro (soit ; il n'y a pas de plus grand élément. De nombreux problèmes demandent de considérer l'ensemble des entiers naturels sans le zéro (soit  - {0}). Cet ensemble est l'ensemble des nombres entiers strictement positifs; il est est noté - {0}). Cet ensemble est l'ensemble des nombres entiers strictement positifs; il est est noté  * ("N étoile") ou * ("N étoile") ou  +. +. On sait qu'il est possible d'ajouter des nombres entiers, de les soustraire, de les multiplier, de les diviser, c'est-à-dire qu'il est possible de pratiquer sur eux certaines opérations dites opérations arithmétiques (on verra plus bas à quoi correspond plus précisément cette expression). Lorsque, par exemple, on additionne deux entiers naturels, le résultat de l'opération est aussi toujours un entier naturel. On peurrait dire la même chose à propos de la multiplication. Mais la situation est différente lorsqu'on soustrait un entier naturel à un autre : dans certains cas le résultat est bien encore un entier naturel (exemple 3 + 4 = 7), mais dans d'autres l'opération de soustraction n'a pas de sens ( exemple 4 - 3 = ?). Pour qu'elle ait un sens, il faut considérer un autre ensemble "plus grand", c'est-à-dire dans lequel  est inclus, ce sera l'ensemble des nombres entiers relatifs. est inclus, ce sera l'ensemble des nombres entiers relatifs. Ensemble des nombre entiers ou nombres entiers relatifs.
L'ensemble des entiers relatifs, nommé  , comprend non seulement tous les entiers naturels ( , comprend non seulement tous les entiers naturels ( 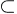  ), mais aussi tous les nombres définis comme le résultat de la soustraction 0 - n, où 0 est le nombre zéro et où n est un entier naturel appartenant à ), mais aussi tous les nombres définis comme le résultat de la soustraction 0 - n, où 0 est le nombre zéro et où n est un entier naturel appartenant à  *. On note ces nombres, en faisant l'économie du zéro : -n (ex : -1, - 7, -12), et on leur donne le nom d'entiers strictement négatifs , et l'ensemble de ces nombres sera noté ici : *. On note ces nombres, en faisant l'économie du zéro : -n (ex : -1, - 7, -12), et on leur donne le nom d'entiers strictement négatifs , et l'ensemble de ces nombres sera noté ici :  -*. -*. L'utilisation que l'on fait ici de l'astérisque signifie que dans notre définition de  -*, on a exclu d'emblée le zéro (l'opération 0 - 0 n'est pas définie, pas plus que le nombre -0). Si l'on parle non plus des entiers strictement négatifs, mais des entiers négatifs, tout court (zéro compris, donc), on pourra adopter pour l'ensemble qui les contient la notation : -*, on a exclu d'emblée le zéro (l'opération 0 - 0 n'est pas définie, pas plus que le nombre -0). Si l'on parle non plus des entiers strictement négatifs, mais des entiers négatifs, tout court (zéro compris, donc), on pourra adopter pour l'ensemble qui les contient la notation :  -. -. Dans le cadre de ce mode de définition, les entiers naturels (qui sont le résultat de l'opération 0 + n) pourront être notés +n. Ecrire +1, +7, +12 est certes une manière compliquée d'écrire 1, 7, 12 , mais cela permet de comprendre pourquoi on donne aussi le nom d'entiers positifs aux entiers naturels. Cela justifie que l'on puisse identifier  l'ensemble que l'on notera l'ensemble que l'on notera  + ( + ( = =  +) et que l'on puisse aussi appeler entiers strictement positifs les éléments de +) et que l'on puisse aussi appeler entiers strictement positifs les éléments de  *= *=  +*. +*.  apparaît dès lors comme la réunion de l'ensemble des entiers naturels (entiers positifs) et de l'ensemble des entiers négatifs : apparaît dès lors comme la réunion de l'ensemble des entiers naturels (entiers positifs) et de l'ensemble des entiers négatifs :
 = =  + +  - -
On notera encore, qu'avec les conventions d'écriture adoptées ici, on a :  + +  - = {0};''' - = {0};''' +* +* ' ' -* = -* =  ; ''' ; ''' z z = =  -*, etc. -*, etc.
Ensemble des nombres rationnels.
On vient de voir comment la soustraction dans l'ensemble des nombres entiers naturels invitait à considérer un ensemble "plus grand", l'ensemble des entiers relatifs. De la même façon, lorsqu'on considère la division '"/" de deux nombres entiers (l'entier par lequel on divise ne pouvant être 0), on constate que l'on ne peut donner de sens à certains résultats appelés quotients (par exemple, -4/2 = -2, est bien un entier (négatif), mais que dire du résultat de 3/2, soit de la division de trois par deux?). On est conduit dès lors à définir l'ensemble  des nombres rationnels comme l'ensemble des nombres qui sont le résultat de la division de deux entiers quelconques. des nombres rationnels comme l'ensemble des nombres qui sont le résultat de la division de deux entiers quelconques. On peut écrire les nombres rationnels comme on vient de le faire, c'est-à-dire comme des fractions, on peut aussi les écrire sous la forme d'un développement décimal dans lequel l'écriture du nombre comprend une partie entière, une virgule et une partie "après la virgule" ou composée de chiffres appelés décimales. Ainsi 3/2 pourra s'écrire 1,5, où 1 est la partie entière et 5 la décimale. De la même façon on pourra écrire 2/3 = 0,66666... Ici la partie entière est 0 et la partie "après la virgule" est composée d'un nombre illimité de décimales.  Les nombres rationnels qui ont seulement zéro pour partie après la virgule correspondent aux nombres entiers (1,0 = 1, -7,0 = -7, etc.; le nombre de zéros étant sans importance : 8 = 8,0 = 8,0000 = 8,000000...). Les nombres rationnels qui ont seulement zéro pour partie après la virgule correspondent aux nombres entiers (1,0 = 1, -7,0 = -7, etc.; le nombre de zéros étant sans importance : 8 = 8,0 = 8,0000 = 8,000000...).  Les nombres rationnels qui on un nombre fini de décimales (par exemple-: 1,5, -3,245) sont appelés nombres décimaux. L'ensemble des nombres décimaux Les nombres rationnels qui on un nombre fini de décimales (par exemple-: 1,5, -3,245) sont appelés nombres décimaux. L'ensemble des nombres décimaux  contient l'ensemble de tous les entiers contient l'ensemble de tous les entiers  , mais n'est qu'un sous-ensemble de , mais n'est qu'un sous-ensemble de  , puisqu'il existe aussi des nombres rationnels qui ont un nombre illimité de décimales, tels que 1/3 = 0,33333... , puisqu'il existe aussi des nombres rationnels qui ont un nombre illimité de décimales, tels que 1/3 = 0,33333...
 Dans l'écriture de tous les nombres rationnels à partir d'un certain moment, les mêmes décimales se répètent (dans le cas d'un nombre décimal, la décimale qui se répète est zéro). Mais quid de nombres tels que Dans l'écriture de tous les nombres rationnels à partir d'un certain moment, les mêmes décimales se répètent (dans le cas d'un nombre décimal, la décimale qui se répète est zéro). Mais quid de nombres tels que = 3,1415926... ou que = 3,1415926... ou que  = 1,4142135...? On pourrait continuer aussi loin que l'on veut, on ne trouvera jamais de répétitions. = 1,4142135...? On pourrait continuer aussi loin que l'on veut, on ne trouvera jamais de répétitions.  et et  n'appartiennent pas à n'appartiennent pas à  , ils ne peuvent pas s'exprimer sous la forme de fractions de nombres entiers. Autrement dit, il existe un ensemble encore "plus grand" que l'ensemble des nombres rationnels... , ils ne peuvent pas s'exprimer sous la forme de fractions de nombres entiers. Autrement dit, il existe un ensemble encore "plus grand" que l'ensemble des nombres rationnels...
Ensemble des nombres réels.
On ne peut pas définir l'ensemble'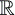 des nombres réels aussi facilement qu'on l'a fait pour les ensembles de nombres précédents. Et, sans doute, constater qu'il existe des nombres qui ne peuvent pas s'écrire sous la forme de fractions d'entiers en en produisant un (ou tant qu'on voudra) peut paraître un peu court pour caractériser des nombres réels aussi facilement qu'on l'a fait pour les ensembles de nombres précédents. Et, sans doute, constater qu'il existe des nombres qui ne peuvent pas s'écrire sous la forme de fractions d'entiers en en produisant un (ou tant qu'on voudra) peut paraître un peu court pour caractériser 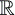 . Mais les différences entre . Mais les différences entre 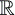 et et  sont assez subtiles et peuvent se comprendre à partir de la distinction que l'on peut faire entre un ensemble dense et un ensemble complet. sont assez subtiles et peuvent se comprendre à partir de la distinction que l'on peut faire entre un ensemble dense et un ensemble complet.  Densité de Densité de  . - Lorsqu'on s'est intéressé aux nombres entiers, on a vu que pour passer d'un nombre au suivant il suffisait d'ajouter un au premier nombre. Deux nombres successifs sont séparés par une unité et, et pour le dire de façon figurée, il n'y a rien entre les deux. Ou si lon veut encore, il y a un espace incompressible entre deux nombres. Les nombres rationnels, des nombres nouveaux sont venus s'intercaler entre les entiers, et l'on pouvent songer à remplir l'intervalle entre deux entiers avec une infinité de nombres rationnels (il suffisait d'augmenter autant qu'on le voulait les décimales). Pour exprimer cela de façon plus mathématique, on dira que cette possibilité tient à ce que . - Lorsqu'on s'est intéressé aux nombres entiers, on a vu que pour passer d'un nombre au suivant il suffisait d'ajouter un au premier nombre. Deux nombres successifs sont séparés par une unité et, et pour le dire de façon figurée, il n'y a rien entre les deux. Ou si lon veut encore, il y a un espace incompressible entre deux nombres. Les nombres rationnels, des nombres nouveaux sont venus s'intercaler entre les entiers, et l'on pouvent songer à remplir l'intervalle entre deux entiers avec une infinité de nombres rationnels (il suffisait d'augmenter autant qu'on le voulait les décimales). Pour exprimer cela de façon plus mathématique, on dira que cette possibilité tient à ce que  (comme l'est aussi d'ailleurs (comme l'est aussi d'ailleurs  ) est un ensemble dense. Un tel ensemble est tel que quels que soient deux de ces éléments, il est toujours possible d'intercaler un élément (et même une infinité d'éléments) entre les deux. ) est un ensemble dense. Un tel ensemble est tel que quels que soient deux de ces éléments, il est toujours possible d'intercaler un élément (et même une infinité d'éléments) entre les deux.  Complétude de Complétude de 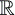 . - Pour en revenir à une expression imagée (et quelque peu aventureuse) de la situation, on pourra dire que dans . - Pour en revenir à une expression imagée (et quelque peu aventureuse) de la situation, on pourra dire que dans  comme dans comme dans 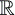 ont pourra avoir deux nombres aussi proches l'un de l'autre que l'on voudra, comme si on pouvait comprimer autant qu'on le voulait l'espace entre les nombres. Dans ont pourra avoir deux nombres aussi proches l'un de l'autre que l'on voudra, comme si on pouvait comprimer autant qu'on le voulait l'espace entre les nombres. Dans  , pourtant, il restera toujours entre deux nombres un interstice (où pourront se glisser des nombres nouveaux comme , pourtant, il restera toujours entre deux nombres un interstice (où pourront se glisser des nombres nouveaux comme  ou ou  par exemple). Dans par exemple). Dans 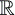 , au contraire, les nombres se touchent. Il ne subiste aucun vide, aucun nombre de manque. Contrairement à , au contraire, les nombres se touchent. Il ne subiste aucun vide, aucun nombre de manque. Contrairement à  , , 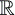 est donc un ensemble complet. Il existe diverses méthodes pour remplir complètement les interstices de est donc un ensemble complet. Il existe diverses méthodes pour remplir complètement les interstices de  et donc construire et donc construire 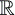 (coupures de Dedekind, séries convergentes de Cauchy); es méthodes permettent de revenir aux vraies mathématiques, dont les deux paragraphes qui précèdent nous ont éloignés. (coupures de Dedekind, séries convergentes de Cauchy); es méthodes permettent de revenir aux vraies mathématiques, dont les deux paragraphes qui précèdent nous ont éloignés.
Ensemble des nombres complexes.
On peut envisager de définir l'ensemble  des nombres complexes un peu à la manière dont on a abordé les définitions de des nombres complexes un peu à la manière dont on a abordé les définitions de  et de et de  . L'introduction de . L'introduction de  provenait du constat que certaines soustractions d'entiers naturels n'étaient pas possibles dans provenait du constat que certaines soustractions d'entiers naturels n'étaient pas possibles dans  ; celle de ; celle de  du constat que la divison de certains entiers n'était pas possible dans du constat que la divison de certains entiers n'était pas possible dans  . . Dans le cas de  , on est invité à s'interroger sur ce qu'il advient si l'on prend la racine carrée d'un nombre réel. La racine carrée de x (notée , on est invité à s'interroger sur ce qu'il advient si l'on prend la racine carrée d'un nombre réel. La racine carrée de x (notée  ) est le nombre y tel que y.y = y² = x. Les règles de la multiplication (.) dans ) est le nombre y tel que y.y = y² = x. Les règles de la multiplication (.) dans 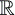 font que x est toujours positif. Un nombre négatif n'a donc pas de racine carrée dans font que x est toujours positif. Un nombre négatif n'a donc pas de racine carrée dans 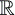 . Il est cependant possible d'introduire un nouveau nombre que l'on notera i et tel que i.i = i² = -1 (écrire i = . Il est cependant possible d'introduire un nouveau nombre que l'on notera i et tel que i.i = i² = -1 (écrire i =  , comme on le fait parfois, s'apparente à ce qu'en grammaire on appellerait un barbarisme). , comme on le fait parfois, s'apparente à ce qu'en grammaire on appellerait un barbarisme). 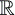 a beau être un ensemble complet i n'appartient pas à l'ensemble des nombres réels; on dit que c'est un nombre imaginaire, c'est même l'unité des nombres imaginaires, tous les autres s'obtenant en multipliant i par un nombre réel. a beau être un ensemble complet i n'appartient pas à l'ensemble des nombres réels; on dit que c'est un nombre imaginaire, c'est même l'unité des nombres imaginaires, tous les autres s'obtenant en multipliant i par un nombre réel.
On dispose à partir de là tous les ingrédients qui permettent de définir l'ensemble  comme l'ensemble de tous les nombres z = a + i.b, où a et b sont des nombres réels. Si a = 0, z est un nombre imaginaire pur, mais si b = 0, a est un nombre réel. Ainsi l'ensemble comme l'ensemble de tous les nombres z = a + i.b, où a et b sont des nombres réels. Si a = 0, z est un nombre imaginaire pur, mais si b = 0, a est un nombre réel. Ainsi l'ensemble 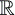 apparaît-il comme un ensemble inclus dans apparaît-il comme un ensemble inclus dans  . On peut d'ailleurs écrire la relation d'inclusion entre les différents ensembles évoqués ici : . On peut d'ailleurs écrire la relation d'inclusion entre les différents ensembles évoqués ici :  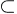  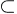  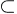 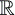 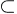  . .
 |
 Gérald Tenenbaum, Michel Mendès France, Les nombres premiers, entre l'ordre et le chaos, Dunod, 2011. -Quoi de plus fascinant que les nombres premiers ? Depuis la plus haute Antiquité, leur suite infinie passionne mathématiciens, philosophes et profanes ; régulière puisque arithmétique, et cependant d'allure chaotique et aléatoire, elle constitue une intarissable source de défis pour l'esprit humain. Longtemps étudiée pour elle-même, la théorie des nombres premiers est aujourd'hui utilisée à la fois comme principe théorique pour des applications à haute valeur ajoutée, telles que la cryptographie, et comme paradigme de système stochastique. La recherche est plus active que jamais dans ce domaine de la théorie des nombres, ainsi qu'en témoignent de récentes et prestigieuses avancées. Cet ouvrage invite le lecteur à une promenade initiatique autour du problème de la répartition des nombres premiers parmi les nombres entiers. Historique et méthodologique, le texte constitue une concise mais solide introduction aux techniques actuelles de la théorie analytique des nombres premiers. Gérald Tenenbaum, Michel Mendès France, Les nombres premiers, entre l'ordre et le chaos, Dunod, 2011. -Quoi de plus fascinant que les nombres premiers ? Depuis la plus haute Antiquité, leur suite infinie passionne mathématiciens, philosophes et profanes ; régulière puisque arithmétique, et cependant d'allure chaotique et aléatoire, elle constitue une intarissable source de défis pour l'esprit humain. Longtemps étudiée pour elle-même, la théorie des nombres premiers est aujourd'hui utilisée à la fois comme principe théorique pour des applications à haute valeur ajoutée, telles que la cryptographie, et comme paradigme de système stochastique. La recherche est plus active que jamais dans ce domaine de la théorie des nombres, ainsi qu'en témoignent de récentes et prestigieuses avancées. Cet ouvrage invite le lecteur à une promenade initiatique autour du problème de la répartition des nombres premiers parmi les nombres entiers. Historique et méthodologique, le texte constitue une concise mais solide introduction aux techniques actuelles de la théorie analytique des nombres premiers.  Alain Bernard, Grégory Chambon, Caroline Ehrhardt, Le sens des nombres : mesures, valeurs et indormations chiffrées : une approche historique, Alain Bernard, Grégory Chambon, Caroline Ehrhardt, Le sens des nombres : mesures, valeurs et indormations chiffrées : une approche historique,
Vuibert, 2010. - En raison d une tradition qui remonte à l'Antiquité, les nombres nous apparaissent souvent comme l'objet privilégié de la pensée mathématique et philosophique. Ce prestige particulier fait pourtant oublier que bien avant qu ils ne deviennent l'objet de spéculations théologiques ou philosophiques les nombres ont d'abord été l'outil de la pensée scientifique et économique et qu ils ont servi à la gestion politique des États. Les nombres sont l'un des instruments avec lesquels, aujourd hui encore, nous appréhendons collectivement la réalité. La longue histoire des nombres et de leur usage ne se réduit pas à la maîtrise d'une série d objets idéaux ou théoriques : elle est complexe et plurimillénaire. C'est à la découverte de cette histoire que cet ouvrage nous invite et c'est en référence directe à des usages qui restent indissociables d'un contexte culturel, social et politique qu il y est question du « sens des nombres ». Toujours accompagnés d'une introduction, les textes historiques réunis dans ce volume sont également pourvus d'un commentaire. Pédagogique, il s'adresse particulièrement aux enseignants et aux formateurs d'enseignants qui s intéressent à la problématique choisie. Quant à cette dernière, exposée en détail dans chaque introduction, elle renvoie aux recherches contemporaines en épistémologie et en histoire des sciences. (couv.).
 John Derbyshire, Dans la jungle des nombres premiers, Dunod, 2007. En 1859, le mathématicien Bernhard Riemann, alors âgé de 33 ans, utilise une hypothèse permettant de trouver combien de nombres premiers sont inférieurs à une certaine valeur. En 1900, l'" hypothèse de Riemann " figure dans la liste des 23 problèmes majeurs du XXe siècle. C'est depuis l'une des plus grandes énigmes mathématiques de tous les temps. Des bataillons de mathématiciens s'y sont attelés, utilisant des ordinateurs de plus en plus sophistiqués. Rien n'y a fait. L'hypothèse de Riemann n'est toujours pas résolue... Et pourtant, les systèmes de cryptographie moderne sont fondés sur cette hypothèse, de même que certaines propriétés physiques de l'atome! L'Institut Clay, aux Etats-Unis, offre un million de dollars à qui trouvera la clé de l'énigme... Cet ouvrage passionnant retrace, dans les chapitres pairs, la saga de cette traque d'un genre bien particulier. Les chapitres impairs, quant à eux, s'adressent aux lecteurs férus de mathématiques. Une véritable plongée dans l'enfer des nombres premiers, pour tous les passionnés de mathématiques ou d'histoire des sciences. (couv.). John Derbyshire, Dans la jungle des nombres premiers, Dunod, 2007. En 1859, le mathématicien Bernhard Riemann, alors âgé de 33 ans, utilise une hypothèse permettant de trouver combien de nombres premiers sont inférieurs à une certaine valeur. En 1900, l'" hypothèse de Riemann " figure dans la liste des 23 problèmes majeurs du XXe siècle. C'est depuis l'une des plus grandes énigmes mathématiques de tous les temps. Des bataillons de mathématiciens s'y sont attelés, utilisant des ordinateurs de plus en plus sophistiqués. Rien n'y a fait. L'hypothèse de Riemann n'est toujours pas résolue... Et pourtant, les systèmes de cryptographie moderne sont fondés sur cette hypothèse, de même que certaines propriétés physiques de l'atome! L'Institut Clay, aux Etats-Unis, offre un million de dollars à qui trouvera la clé de l'énigme... Cet ouvrage passionnant retrace, dans les chapitres pairs, la saga de cette traque d'un genre bien particulier. Les chapitres impairs, quant à eux, s'adressent aux lecteurs férus de mathématiques. Une véritable plongée dans l'enfer des nombres premiers, pour tous les passionnés de mathématiques ou d'histoire des sciences. (couv.).
 Gérald Tenenbaum, Introduction à la théorie analytique et probabiliste des nombres, Belin, 2008. - "La mathématique est la reine des sciences et la théorie des nombres est la reine des mathématiques" disait Gauss. Parfaitement dans l'esprit de la collection "Echelles", l'ouvrage de G. Tenenbaum est une excellente introduction à l'application des méthodes de l'analyse et des probabilités à la théorie des nombres (autrement dit "l'arithmétique", la sciences des entiers positifs ou négatifs). (couv.). Gérald Tenenbaum, Introduction à la théorie analytique et probabiliste des nombres, Belin, 2008. - "La mathématique est la reine des sciences et la théorie des nombres est la reine des mathématiques" disait Gauss. Parfaitement dans l'esprit de la collection "Echelles", l'ouvrage de G. Tenenbaum est une excellente introduction à l'application des méthodes de l'analyse et des probabilités à la théorie des nombres (autrement dit "l'arithmétique", la sciences des entiers positifs ou négatifs). (couv.).
 Marcus du Sautoy, La symphonie des nombres premiers, Eloïse d'Ormesson, 2006. --Les nombres premiers donnent l'impression d'apparaître au hasard dans la suite des nombres entiers. Depuis des siècles, les mathématiciens s'échinent à en percer le secret. S'appuyant sur les arcanes de ce mystère, du Sautoy traite la question en détective. Sa Symphonie des nombres premiers se lit comme un polar qui débuterait en 1859, lorsque Riemann formule une hypothèse selon laquelle l'apparition des nombres premiers suivrait la partition d'un orchestre mathématique. Mais Riemann laisse sa thèse inachevée. (couv.). Marcus du Sautoy, La symphonie des nombres premiers, Eloïse d'Ormesson, 2006. --Les nombres premiers donnent l'impression d'apparaître au hasard dans la suite des nombres entiers. Depuis des siècles, les mathématiciens s'échinent à en percer le secret. S'appuyant sur les arcanes de ce mystère, du Sautoy traite la question en détective. Sa Symphonie des nombres premiers se lit comme un polar qui débuterait en 1859, lorsque Riemann formule une hypothèse selon laquelle l'apparition des nombres premiers suivrait la partition d'un orchestre mathématique. Mais Riemann laisse sa thèse inachevée. (couv.).
| | |